题目内容
5. 在平面直角坐标系xOy中,二次函数y=(a-1)x2+2x+1与x轴有交点,a为正整数.
在平面直角坐标系xOy中,二次函数y=(a-1)x2+2x+1与x轴有交点,a为正整数.(1)求a的值.
(2)将二次函数y=(a-1)x2+2x+1的图象向右平移m个单位,向下平移m2+1个单位,当-2≤x≤1时,二次函数有最小值-3,求实数m的值.
分析 (1)根据二次函数y=(a-1)x2+2x+1与x轴有交点,令y=0,则(a-1)x2+2x+1=0,△≥0,求出a的取值范围,再根据a为正整数求出a的值;
(2)根据(1)中a的值得出二次函数的表达式,根据二次函数平移的性质得出其顶点坐标,再由二次函数有最小值-3即可得出结论.
解答 解:(1)∵二次函数y=(a-1)x2+2x+1与x轴有交点,
令y=0,则(a-1)x2+2x+1=0,
∴△=4-4(a-1)≥0,解得a≤2.
∵a为正整数,
∴a=1、2
又∵y=(a-1)x2+2x+1是二次函数,∴a-1≠0,∴a≠1,
∴a的值为2.
(2)∵a=2,
∴二次函数表达式为y=x2+2x+1,将二次函数y=x2+2x+1化成顶点式y=(x+1)2,二次函数图象向右平移m个单位,向下平移m2+1个单位后的表达式为y=(x+1-m)2-(m2+1).此时函数的顶点坐标为(m-1,-m2-1).
当m-1<-2,即m<-1时,x=-2时,二次函数有最小值-3,
∴-3=(-1-m)2-(m2+1),解得m=-$\frac{3}{2}$且符合题目要求.
当-2≤m-1≤1,即-1≤m≤2,时,当 x=m-1时,二次函数有最小值-m2-1=-3,
解得m=±$\sqrt{2}$.
∵m=-$\sqrt{2}$不符合-1≤m≤2的条件,舍去.
∴m=$\sqrt{2}$.
当m-1>1,即m>2时,当 x=1时,二次函数有最小值-3,
∴-3=(2-m)2-(m2+1),解得m=$\frac{3}{2}$,不符合m>2的条件舍去.
综上所述,m的值为-$\frac{3}{2}$或$\sqrt{2}$.
点评 本题考查的是抛物线与x轴的交点,熟知二次函数的图象与x轴的交点与△的关系是解答此题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | b=0 | B. | b=-1 | C. | b=2 | D. | b=-2 |
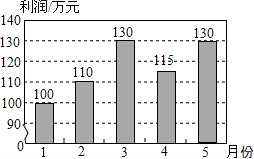 某企业1~5月份的利润情况如图所示,则下列说法中正确的是( )
某企业1~5月份的利润情况如图所示,则下列说法中正确的是( )| A. | 1~2月份利润的增长快于2~3月份利润的增长 | |
| B. | 1~4月份利润的极差于1~5月份利润的极差不同 | |
| C. | 1~5月份利润的中位数是120万元 | |
| D. | 1~5月份利润的众数是130万元 |
| 电视机 | 洗衣机 | |
| 进价/(元/台) | 1800 | 1500 |
 如图,在?ABCD中,O为对角线AC的中点,EF经过点O并与AB,CD分别相交于点E,F.
如图,在?ABCD中,O为对角线AC的中点,EF经过点O并与AB,CD分别相交于点E,F.