题目内容
20.解三元一次方程组:$\left\{\begin{array}{l}{2x+y+z=15}\\{x+2y+z=16}\\{x+y+2z=17}\end{array}\right.$.分析 先消掉y,再组成关于x、z的方程组,求出x、z,代入即可求出y的值;
解答 解:$\left\{\begin{array}{l}{2x+y+z=15①}\\{x+2y+z=16②}\\{x+y+2z=17③}\end{array}\right.$,
由①-③,得
x-z=-2,④
由③×2-②,得
x+3z=18,⑤
由④-⑤,解得z=5.
把z=5代入④,得
x=3.
把x=3,z=5代入①得到:y=4.
所以原方程组的解为:$\left\{\begin{array}{l}{x=3}\\{y=4}\\{z=5}\end{array}\right.$.
点评 本题考查了解三元一次方程组,先转化为二元一次方程组,求出二元一次方程组的解,再求出第三个未知数的值.

练习册系列答案
相关题目
15.某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机的进货量不少于洗衣机的进货量的一半,电视机和洗衣机的进价如表:
计划购进电视机和洗衣机共100台,商店最多可筹集资金161800元,请你帮助商店算一算共有多少种进货方案.(不考虑除进价之外的其它费用)
| 电视机 | 洗衣机 | |
| 进价/(元/台) | 1800 | 1500 |
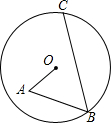 如图所示,⊙O内有折线OABC,其中OA=2,AB=4,∠A=∠B=60°,则BC的长为6.
如图所示,⊙O内有折线OABC,其中OA=2,AB=4,∠A=∠B=60°,则BC的长为6.