题目内容
3.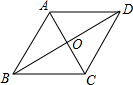 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 首先根据菱形的性质知AC垂直平分BD,再证出△ABC是正三角形,由三角函数求出BO,即可求出BD的长.
解答 解:∵四边形ABCD菱形,
∴AC⊥BD,BD=2BO,
∵∠ABC=60°,
∴△ABC是正三角形,
∴∠BAO=60°,
∴BO=sin60°•AB=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴BD=2$\sqrt{3}$.
故选:D.
点评 本题主要考查解直角三角形和菱形的性质的知识点,解答本题的关键是熟记菱形的对角线垂直平分,本题难度一般.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13. 已知一次函数y=kx+b的图象如图所示,当x<2时,y的取值范围是( )
已知一次函数y=kx+b的图象如图所示,当x<2时,y的取值范围是( )
 已知一次函数y=kx+b的图象如图所示,当x<2时,y的取值范围是( )
已知一次函数y=kx+b的图象如图所示,当x<2时,y的取值范围是( )| A. | y<-4 | B. | -4<y<0 | C. | y<2 | D. | y<0 |
14. 如图,在数轴上表示某不等式组中的两个不等式的解集,则该不等式组的解集为( )
如图,在数轴上表示某不等式组中的两个不等式的解集,则该不等式组的解集为( )
 如图,在数轴上表示某不等式组中的两个不等式的解集,则该不等式组的解集为( )
如图,在数轴上表示某不等式组中的两个不等式的解集,则该不等式组的解集为( )| A. | x≤-2 | B. | x≥3 | C. | 3≤x≤-2 | D. | -2≤x≤3 |
4.$\left\{\begin{array}{l}{0.2x-0.3y=2}\\{0.2x-0.7y=-1.5}\end{array}\right.$最适合用的方法是( )
| A. | 换元法 | B. | 加减消元法 | C. | 代入消元法 | D. | 无法确定 |
 如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:
如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论: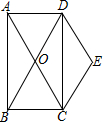 如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.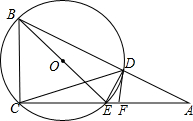 如图,在Rt△ACB中,∠A=30°,过点B、C的⊙O交AB于D,交AC于E,点F在AE上,连接DE、DC、BE和DF,已知BC=EC,AD=AF.
如图,在Rt△ACB中,∠A=30°,过点B、C的⊙O交AB于D,交AC于E,点F在AE上,连接DE、DC、BE和DF,已知BC=EC,AD=AF. 如图,在?ABCD中,点E,M分别在边AB,CD上,且AE=CM,点F,N分别在边BC,AD上,且DN=BF.
如图,在?ABCD中,点E,M分别在边AB,CD上,且AE=CM,点F,N分别在边BC,AD上,且DN=BF.