题目内容
18.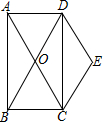 如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
分析 (1)根据平行四边形的判定得出四边形OCED是平行四边形,根据矩形的性质求出OC=OD,根据菱形的判定得出即可.
(2)解直角三角形求出BC=2.AB=DC=2$\sqrt{3}$,连接OE,交CD于点F,根据菱形的性质得出F为CD中点,求出OF=$\frac{1}{2}$BC=1,求出OE=2OF=2,求出菱形的面积即可.
解答 (1)证明:∵CE∥OD,DE∥OC,
∴四边形OCED是平行四边形,
∵矩形ABCD,∴AC=BD,OC=$\frac{1}{2}$AC,OD=$\frac{1}{2}$BD,
∴OC=OD,
∴四边形OCED是菱形;
(2)解:在矩形ABCD中,∠ABC=90°,∠BAC=30°,AC=4,
∴BC=2,
∴AB=DC=2$\sqrt{3}$,
连接OE,交CD于点F,
∵四边形ABCD为菱形,
∴F为CD中点,
∵O为BD中点,
∴OF=$\frac{1}{2}$BC=1,
∴OE=2OF=2,
∴S菱形OCED=$\frac{1}{2}$×OE×CD=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$.
点评 本题考查了矩形的性质和菱形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:菱形的面积等于对角线积的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知在平面直角坐标系中,点A的坐标为(3,0),点B的坐标为(0,4),连接AB,现将线段AB进行平移,平移后得到点B的对应点D的坐标为(1,5),则点A的对应点C的坐标为( )
| A. | (3,0) | B. | (4,1) | C. | (2,-1) | D. | (0,5) |
9.某班为奖励在校运动会上取得好成绩的同学,花了200元钱购买甲、乙两种奖品共30件,其中甲种奖品每件8元,乙种奖品每件6元.若设购买甲种奖品x件,乙种奖品y件,则所列方程正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=30}\\{6x+8y=200}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=30}\\{8x+6y=200}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{6x+8y=30}\\{x+y=200}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{8x+6y=30}\\{x+y=200}\end{array}\right.$ |
3.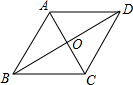 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )
 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |