题目内容
5.一个直角三角形的两条直角边分别为6和8,那么这个直角三角形斜边上的高为4.8.分析 根据勾股定理可求出斜边.然后由于同一三角形面积一定,可列方程直接解答.
解答 解:∵直角三角形的两条直角边分别为6,8,
∴斜边为$\sqrt{{6}^{2}+{8}^{2}}$=10,
设斜边上的高为h,
则直角三角形的面积为$\frac{1}{2}$×6×8=$\frac{1}{2}$×10h,h=4.8,
这个直角三角形斜边上的高为4.8,
故答案为4.8.
点评 本题考查了勾股定理的运用,即直角三角形的面积的求法,求出斜边长是关键,属中学阶段常见的题目,需同学们认真掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.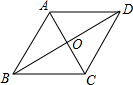 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )
 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为( )| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
14.下列各组数是三角形的三边,能组成直角三角形的一组数是( )
| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 2,3,4 | C. | 3,4,5 | D. | 6,8,12 |
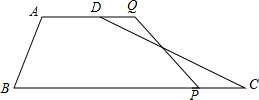 如图,在四边形ABCD中,AD∥BC AD=5cm,BC=8cm,M是CD的中点,P是BC边上一个动点(P与B,C不重合)连接PM并延长交AD的延长线于Q.
如图,在四边形ABCD中,AD∥BC AD=5cm,BC=8cm,M是CD的中点,P是BC边上一个动点(P与B,C不重合)连接PM并延长交AD的延长线于Q. 如图,已知BC∥DE,∠ABC=120°,那么直线AB、DE的夹角是120°或60°.
如图,已知BC∥DE,∠ABC=120°,那么直线AB、DE的夹角是120°或60°.