题目内容
1.解方程组:$\left\{\begin{array}{l}{0=a-b+c}\\{0=25a+5b+c}\\{-c=\frac{5}{2}}\end{array}\right.$.分析 解决本题关键是寻找式子间的关系,寻找方法降元,①×5+②可化去b,其它即可得解.
解答 解:$\left\{\begin{array}{l}{0=a-b+c①}\\{0=25a+5b+c②}\\{-c=\frac{5}{2}③}\end{array}\right.$
①×5+②得30a+6c=0④,
由③得c=-$\frac{5}{2}$代入④得:a=$\frac{1}{2}$,
∴b=-2.
∴方程组的解为$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-2}\\{c=-\frac{5}{2}}\end{array}\right.$.
点评 本题考查了三元一次方程组的解法,有加减法和代入法两种,本题灵活运用代入消元法是解题的关键.

练习册系列答案
相关题目
11.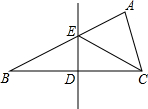 如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
 如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )| A. | 1 | B. | 1+$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
12.现有四把钥匙去开一把锁,其中只有二把钥匙能开这把锁,一个人随机拿其中一把钥匙开锁,若不能开则把这把钥匙扔掉,则这个人用这四把钥匙到第三次才能打开这把锁的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{5}$ |
6.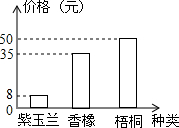 为了响应市政府提出的“创建森林城市”的号召,市林业局计划今年在瓯江口新区种植梧桐、紫玉兰和香樟三类树苗,其中香樟树苗的株数是梧桐树苗的2倍,三种树苗的单价如图所示,设计划种植x株梧桐树苗,y株紫玉兰树苗;
为了响应市政府提出的“创建森林城市”的号召,市林业局计划今年在瓯江口新区种植梧桐、紫玉兰和香樟三类树苗,其中香樟树苗的株数是梧桐树苗的2倍,三种树苗的单价如图所示,设计划种植x株梧桐树苗,y株紫玉兰树苗;
(1)根据信息,完成表格:
(2)若三种树苗共种植150株,购买树苗共花费5040元,那么三种树苗分别种植了多少株?
(3)若购买树苗的总费用是7232元,那么最少能种植树苗64株.
 为了响应市政府提出的“创建森林城市”的号召,市林业局计划今年在瓯江口新区种植梧桐、紫玉兰和香樟三类树苗,其中香樟树苗的株数是梧桐树苗的2倍,三种树苗的单价如图所示,设计划种植x株梧桐树苗,y株紫玉兰树苗;
为了响应市政府提出的“创建森林城市”的号召,市林业局计划今年在瓯江口新区种植梧桐、紫玉兰和香樟三类树苗,其中香樟树苗的株数是梧桐树苗的2倍,三种树苗的单价如图所示,设计划种植x株梧桐树苗,y株紫玉兰树苗;(1)根据信息,完成表格:
| 梧桐 | 香樟 | 紫玉兰 | 合计 | |
| 树苗株数 | x | 2x | y | 3x+y |
| 费用 | 50x | 70x | 8y | 120x+8y |
(3)若购买树苗的总费用是7232元,那么最少能种植树苗64株.
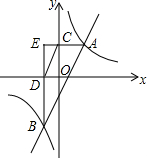 如图,反比例函数y=$\frac{k}{x}$(k>0)与一次函数y=ax-2(a>0)的图象都经过点A、B,过点A作AC⊥y轴与点C,过点B作BD⊥x轴于点D.
如图,反比例函数y=$\frac{k}{x}$(k>0)与一次函数y=ax-2(a>0)的图象都经过点A、B,过点A作AC⊥y轴与点C,过点B作BD⊥x轴于点D.
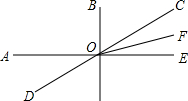 已知,OB⊥AE于点O,OF平分∠COE,∠AOF=$\frac{3}{2}$∠BOF,求证:∠BOD的度数.
已知,OB⊥AE于点O,OF平分∠COE,∠AOF=$\frac{3}{2}$∠BOF,求证:∠BOD的度数.