题目内容
12．现有四把钥匙去开一把锁，其中只有二把钥匙能开这把锁，一个人随机拿其中一把钥匙开锁，若不能开则把这把钥匙扔掉，则这个人用这四把钥匙到第三次才能打开这把锁的概率为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{5}$ |
分析 首先分别用A，B，C，D表示四把钥匙，用A，B分别表示二把钥匙能开这把锁，然后根据题意画树状图，由树状图求得所有等可能的结果与这个人用这四把钥匙到第三次才能打开这把锁的情况，再利用概率公式即可求得答案．
解答 解：分别用A，B，C，D表示四把钥匙，用A，B分别表示二把钥匙能开这把锁，
画树状图得：
∵共有24种等可能的结果，这个人用这四把钥匙到第三次才能打开这把锁的4种情况，
∴这个人用这四把钥匙到第三次才能打开这把锁的概率为：$\frac{4}{24}$=$\frac{1}{6}$．
故选C．
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
名校课堂系列答案
相关题目
2．
如图，⊙O是△ABC的外接圆，已知∠A=30°，BC=2，则⊙O的半径为（ ）
如图，⊙O是△ABC的外接圆，已知∠A=30°，BC=2，则⊙O的半径为（ ）| A． | 1 | B． | 2 | C． | $\sqrt{3}$ | D． | 4 |
如图，在平面直角坐标系中，四边形OABC的顶点O为坐标原点，点C在x轴的正半轴上，且BC⊥OC于点C，点A的坐标为（2，2$\sqrt{3}$），AB=4$\sqrt{3}$，∠B=60°，点D是线段OC上一点，且OD=4，连接AD．
如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且∠ABC+∠ADC=180°．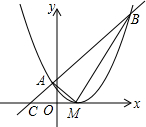
抛物线y=$\frac{1}{2}$（x-1）2，顶点为M，直线AB交抛物线于A、B两点，且MA⊥MB，求证：直线AB过定点．
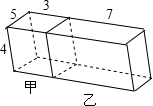如图，长10m、宽5m、深4m的长方体水池被隔成底面积分别是3m×5m和7m×5m的甲、乙两池（设隔墙厚度忽略不计），两池隔墙下方有阀门相连．