题目内容
13.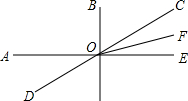 已知,OB⊥AE于点O,OF平分∠COE,∠AOF=$\frac{3}{2}$∠BOF,求证:∠BOD的度数.
已知,OB⊥AE于点O,OF平分∠COE,∠AOF=$\frac{3}{2}$∠BOF,求证:∠BOD的度数.
分析 首先根据角平分线的性质可得∠COF=∠FOE=$\frac{1}{2}∠$COE,然后设∠EOF=x°,则∠AOC=(180-x)°,∠BOF=(90-x)°,进而可得方程180-x=$\frac{3}{2}$(90-x),计算出x的值,然后可得∠COE的度数,再可得∠BOD的度数.
解答 解:∵OF平分∠COE,
∴∠COF=∠FOE=$\frac{1}{2}∠$COE,
∵OB⊥AE,
∴∠AOB=∠BOE=90°,
设∠EOF=x°,则∠AOC=(180-x)°,∠BOF=(90-x)°,
∵∠AOF=$\frac{3}{2}$∠BOF,
∴180-x=$\frac{3}{2}$(90-x),
解得:x=22.5,
∴∠COE=45°,
∴∠AOD=45°,
∴∠BOD=90°+45°=135°.
点评 此题主要考查了垂线和角平分线的性质,关键是利用方程思想计算出∠EOF的度数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC于点C,点A的坐标为(2,2$\sqrt{3}$),AB=4$\sqrt{3}$,∠B=60°,点D是线段OC上一点,且OD=4,连接AD.
如图,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且BC⊥OC于点C,点A的坐标为(2,2$\sqrt{3}$),AB=4$\sqrt{3}$,∠B=60°,点D是线段OC上一点,且OD=4,连接AD.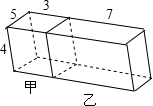 如图,长10m、宽5m、深4m的长方体水池被隔成底面积分别是3m×5m和7m×5m的甲、乙两池(设隔墙厚度忽略不计),两池隔墙下方有阀门相连.
如图,长10m、宽5m、深4m的长方体水池被隔成底面积分别是3m×5m和7m×5m的甲、乙两池(设隔墙厚度忽略不计),两池隔墙下方有阀门相连.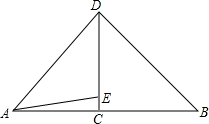 重庆市是著名的山城,许多美丽的建筑建在山上,如图,刘老师为了测量小山项一建筑物DE的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的A处测得建筑物顶端D的仰角为53°,山坡AE的坡度i=1:5,潘老师在B处测得建筑物顶端D的仰角为45°.若此时刘老师与潘老师的距离AB=200m,求建筑物DE的高度.(sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,结果精确到0.1m)
重庆市是著名的山城,许多美丽的建筑建在山上,如图,刘老师为了测量小山项一建筑物DE的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的A处测得建筑物顶端D的仰角为53°,山坡AE的坡度i=1:5,潘老师在B处测得建筑物顶端D的仰角为45°.若此时刘老师与潘老师的距离AB=200m,求建筑物DE的高度.(sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,结果精确到0.1m)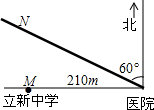 如图,立新中学(用点M表示)位于医院(用点O表示)的正西面210米处,经过医院且沿北偏西60°方向有一条公路ON,公路上行驶车辆的噪音范围一般在120米内.
如图,立新中学(用点M表示)位于医院(用点O表示)的正西面210米处,经过医院且沿北偏西60°方向有一条公路ON,公路上行驶车辆的噪音范围一般在120米内.