题目内容
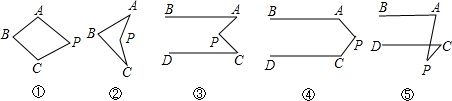
16.(1)四边形ABCP,如图①,当点P沿PB方向靠近B时,得到图②,此时∠APC与∠ABC、∠A、∠C是什么关系?(2)当A,P,C不动时,将B向左拉向无穷远处,使AB∥DC,得到图③,此时∠APC与∠A,∠C是什么关系?
(3)当AB,CD不动时,将P向右拉动得到图④,此时∠APC与∠A,∠C是什么关系?
(4)当固定AB,CD,将点P拉向其它位置时(如图⑤),你能得到其他的什么猜想?
分析 (1)连接BP并延长,根据三角形外角的性质即可得出结论;
(2)过点P作PE∥DC,根据平行线的性质即可得出结论;
(3)过点P作PE∥DC,根据平行线的性质可得出AB∥PE,进而可得出结论;
(4)先根据平行线的性质得出∠A=∠AEC,再由三角形外角的性质即可得出结论.
解答 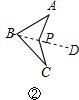 解:(1)∠APC=∠B+∠A+∠C.
解:(1)∠APC=∠B+∠A+∠C.
连接BP并延长,
∵∠APD=∠A+∠ABP,∠CPD=∠C+∠CBD,
∴∠APC=∠B+∠A+∠C;
(2)∠APC=∠A+∠C.
理由:如图③,过点P作PE∥DC,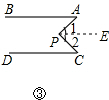
∵AB∥DC,PE∥DC,
∴AB∥PE.
∵PE∥DC,AB∥PE,
∴∠1=∠A,∠2=∠C,
∴∠APC=∠A+∠C;
(3)∠APC+∠A+∠C=360°.
过点P作PE∥DC,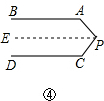
∵AB∥DC,PE∥DC,
∴AB∥PE.
∵PE∥DC,AB∥PE
∴∠A+∠APE=180°,∠C+∠EPC=180°,
∴∠APC+∠A+∠C=360°;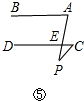
(4)∠P+∠C=∠A.
∵AB∥CD,
∴∠A=∠AEC,
∵∠AEC是△PCE的外角,
∴∠AEC=∠P+∠C,即∠P+∠A=∠C.
点评 本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 完成下列证明过程,并在括号中注明理由.
完成下列证明过程,并在括号中注明理由.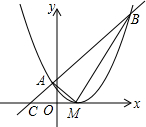 抛物线y=$\frac{1}{2}$(x-1)2,顶点为M,直线AB交抛物线于A、B两点,且MA⊥MB,求证:直线AB过定点.
抛物线y=$\frac{1}{2}$(x-1)2,顶点为M,直线AB交抛物线于A、B两点,且MA⊥MB,求证:直线AB过定点.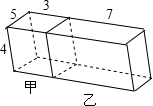 如图,长10m、宽5m、深4m的长方体水池被隔成底面积分别是3m×5m和7m×5m的甲、乙两池(设隔墙厚度忽略不计),两池隔墙下方有阀门相连.
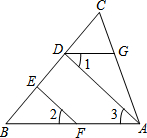
如图,长10m、宽5m、深4m的长方体水池被隔成底面积分别是3m×5m和7m×5m的甲、乙两池(设隔墙厚度忽略不计),两池隔墙下方有阀门相连. 如图,已知?ABCD中,AE⊥BC,点E是垂足,AE与BD交于点G,且DG=2AB,∠DBC=25°.求∠ABD的度数.
如图,已知?ABCD中,AE⊥BC,点E是垂足,AE与BD交于点G,且DG=2AB,∠DBC=25°.求∠ABD的度数.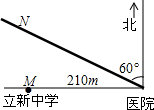 如图,立新中学(用点M表示)位于医院(用点O表示)的正西面210米处,经过医院且沿北偏西60°方向有一条公路ON,公路上行驶车辆的噪音范围一般在120米内.
如图,立新中学(用点M表示)位于医院(用点O表示)的正西面210米处,经过医院且沿北偏西60°方向有一条公路ON,公路上行驶车辆的噪音范围一般在120米内.