题目内容
6.已知二次函数y=ax2+2ax-(a+m)的图象经过点P(2,5),交x轴于点A(x1,0),B(x2,0),且x1<0<x2,满足OA=3OB,求此二次函数的解析式.分析 由于x1<0<x2,OA=3OB,则-x1=3x2,再由根与系数的关系得到x1+x2=-2,则可解出x2=1,x1=-3,即A(-3,0),B(1,0),然后设交点式y=a(x+3)(x-1),再把P点坐标代入求出a即可.
解答 解:∵x1<0<x2,OA=3OB,
∴-x1=3x2,即x1=-3x2,
∵x1+x2=-$\frac{2a}{a}$=-2,
∴-3x2+x2=-2,解得x2=1,
∴x1=-3x2=-3,
∴A(-3,0),B(1,0),
设抛物线解析式为y=a(x+3)(x-1),
把P(2,5)代入得a•5•1=-5,
解得a=1,
∴抛物线解析式为y=(x+3)(x-1)=x2+2x-3.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了根与系数的关系.

练习册系列答案
相关题目
14.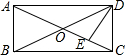 如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
 如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )| A. | 36° | B. | 9° | C. | 27° | D. | 18° |
1.已知点P是矩形ABCD内一点,连结AP、BP、CP、DP,若S△ABP+S△CDP=S△ADP+S△BCP,则关于点P的位置,正确的说法是( )
| A. | 一定是对角线交点 | B. | 一定在对角线上 | ||
| C. | 一定在对边中点的连线上 | D. | 可以是任意位置 |
11. 如图,已知点A、B、C、D在同一直线上,△AEC≌△DFB,如果AD=37cm,BC=15cm,那么AB的长为( )
如图,已知点A、B、C、D在同一直线上,△AEC≌△DFB,如果AD=37cm,BC=15cm,那么AB的长为( )
 如图,已知点A、B、C、D在同一直线上,△AEC≌△DFB,如果AD=37cm,BC=15cm,那么AB的长为( )
如图,已知点A、B、C、D在同一直线上,△AEC≌△DFB,如果AD=37cm,BC=15cm,那么AB的长为( )| A. | 10cm | B. | 11cm | C. | 12cm | D. | 13cm |
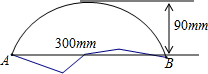 一支考古队发现一个残破的古代圆盘碎片,如图所示,考古家测量了弦AB=300mm,圆弧的高为90mm,于是得到了古圆盘的半径,从而确定了它的圆心,终于使这个古物得以复原,请问你知道考古家怎样得到它的半径吗?
一支考古队发现一个残破的古代圆盘碎片,如图所示,考古家测量了弦AB=300mm,圆弧的高为90mm,于是得到了古圆盘的半径,从而确定了它的圆心,终于使这个古物得以复原,请问你知道考古家怎样得到它的半径吗?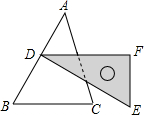 如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,且BC∥DF.若∠A=50°,则∠C的度数为70°.
如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,且BC∥DF.若∠A=50°,则∠C的度数为70°.