题目内容
16.$\frac{1}{1×2}=1-\frac{1}{2}$,$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$.将以上三个等式两边分别相加得:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$.
(1)猜想并写出:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)直接写出下列各式的计算结果:
①$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2006×2007}$=$\frac{2006}{2007}$;
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$=$\frac{n}{n+1}$;
(3)探究并计算:
①$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2006×2008}$
②$\frac{1}{1×4}$+$\frac{1}{4×7}$+$\frac{1}{7×10}$+$\frac{1}{10×13}$+$\frac{1}{13×16}$+$\frac{1}{16×19}$.
分析 (1)根据已知等式猜想得到拆项规律,写出即可;
(2)原式各项利用得出的拆项规律变形,计算即可得到结果;
(3)原式各项利用得出的拆项规律变形,计算即可得到结果.
解答 解:(1)$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)①原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2006}$-$\frac{1}{2007}$=1-$\frac{1}{2007}$=$\frac{2006}{2007}$;
②原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$;
(3)①原式=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{2006}$-$\frac{1}{2008}$)=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{2008}$)=$\frac{1003}{4016}$;
②原式=$\frac{1}{3}$(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+…+$\frac{1}{16}$-$\frac{1}{19}$)=$\frac{1}{2}$(1-$\frac{1}{19}$)=$\frac{9}{19}$.
故答案为:(1)$\frac{1}{n}$-$\frac{1}{n+1}$;(2)①$\frac{2006}{2007}$;②$\frac{n}{n+1}$
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

 名校课堂系列答案
名校课堂系列答案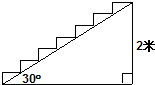 如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )
如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )| A. | 2($\sqrt{3}$+1)m | B. | 4m | C. | ($\sqrt{3}$+2)m | D. | 2($\sqrt{3}$+3)m |
| A. | 0 | B. | -4 | C. | 1 | D. | -4和0 |
| A. | a+b=b+a | B. | |a|≥0 | C. | 1 | D. | x≠0 |
 如图,一个几何体的主视图和左视图相同.则摆成这个几何体最少需要4个小正方体.
如图,一个几何体的主视图和左视图相同.则摆成这个几何体最少需要4个小正方体.