题目内容
17.已知a<0,b>0,且a2+5a=$\frac{1}{b}$+$\frac{5}{\sqrt{b}}$=1,则代数式$\frac{{a}^{3}b\sqrt{b}+1}{b\sqrt{b}}$的值为-140.分析 首先利用一元二次方程根的性质结合根与系数的关系得出a+$\frac{1}{\sqrt{b}}$=-5,a•$\frac{1}{\sqrt{b}}$=-1,进而将原式变形利用所求代入求出即可.
解答 解:由题意可知:a,$\frac{1}{\sqrt{b}}$是一元二次方程x2+5x-1=0的两根,
故a+$\frac{1}{\sqrt{b}}$=-5,a•$\frac{1}{\sqrt{b}}$=-1,
则$\frac{{a}^{3}b\sqrt{b}+1}{b\sqrt{b}}$
=a3+($\frac{1}{\sqrt{b}}$)3
=(a+$\frac{1}{\sqrt{b}}$)(a2-a•$\frac{1}{\sqrt{b}}$+$\frac{1}{b}$)
=-5×[(a+$\frac{1}{\sqrt{b}}$)2-3a•$\frac{1}{\sqrt{b}}$]
=-5×[(-5)2-3×(-1)]
=-140.
故答案为:-140.
点评 此题主要考查了二次根式的化简求值以及根与系数的关系,正确根据根与系数关系求出是解题关键.

练习册系列答案
相关题目
7.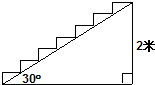 如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )
如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )
 如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )
如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )| A. | 2($\sqrt{3}$+1)m | B. | 4m | C. | ($\sqrt{3}$+2)m | D. | 2($\sqrt{3}$+3)m |
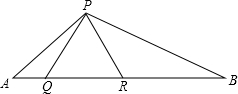 如图所示,已知△PQR是等边三角形,∠APB=120°.
如图所示,已知△PQR是等边三角形,∠APB=120°.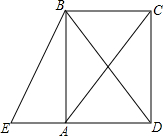 如图,四边形ABCD是矩形,延长DA至点E,使得AC=BE.
如图,四边形ABCD是矩形,延长DA至点E,使得AC=BE.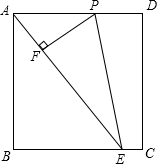 如图,矩形ABCD中,AB=4,E是BC边上一点,且BE=3,点P是射线AD上的一个动点,过点P作PF⊥AE,垂足为F,连接PE.
如图,矩形ABCD中,AB=4,E是BC边上一点,且BE=3,点P是射线AD上的一个动点,过点P作PF⊥AE,垂足为F,连接PE.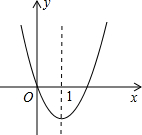 二次函数y=x2+bx的图象如图所示,对称轴为直线x=1.
二次函数y=x2+bx的图象如图所示,对称轴为直线x=1.