题目内容
1.已知点P是矩形ABCD内一点,连结AP、BP、CP、DP,若S△ABP+S△CDP=S△ADP+S△BCP,则关于点P的位置,正确的说法是( )| A. | 一定是对角线交点 | B. | 一定在对角线上 | ||
| C. | 一定在对边中点的连线上 | D. | 可以是任意位置 |
分析 作PE⊥AD于E,延长EP交BC于F,则PF⊥BC,EF=AB,证出△ADP的面积+△BCP的面积=$\frac{1}{2}$矩形ABCD的面积,同理得出△ABP的面积+△CDP的面积=$\frac{1}{2}$矩形ABCD的面积,即可得出结论.
解答 解:∵四边形ABCD是矩形,
∴AD=BC,AB=CD,
作PE⊥AD于E,延长EP交BC于F,如图所示:
则PF⊥BC,EF=AB,
∵△ADP的面积+△BCP的面积=$\frac{1}{2}$AD•PE+$\frac{1}{2}$BC•PF=$\frac{1}{2}$BC(PE+PF)=$\frac{1}{2}$BC•EF=$\frac{1}{2}$BC•AB,
∴△ADP的面积+△BCP的面积=$\frac{1}{2}$矩形ABCD的面积,
同理:△ABP的面积+△CDP的面积=$\frac{1}{2}$矩形ABCD的面积,
∴△ADP的面积+△BCP的面积=△ABP的面积+△CDP的面积;
故选:D.
点评 本题考查了矩形的性质、三角形面积的计算;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
9.下列式子总有意义的是( )
| A. | $\sqrt{a}$ | B. | $\sqrt{-a}$ | C. | $\sqrt{-{a}^{2}}$ | D. | $\sqrt{|a|}$ |
16.某市举行中学生“奋发有为建小康”演讲比赛,某同学将选手的得分情况进行统计,绘成如图所示的得分成绩统计图,下列四个论断:①众数为6分;②有8名选手的成绩高于8分;③中位数是8分;④得6分和9分的人数一样多,其中正确的是( )
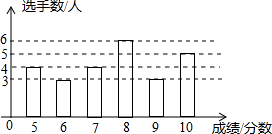

| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①②③④ |
10.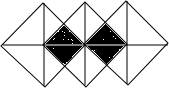 如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )
如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )
 如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )
如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
11.已知a、b互为相反数,c、d互为倒数,m的绝对值为2,$\frac{a+b}{m}$+m-2cd的值( )
| A. | 0 | B. | -4 | C. | 1 | D. | -4和0 |
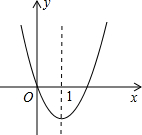 二次函数y=x2+bx的图象如图所示,对称轴为直线x=1.
二次函数y=x2+bx的图象如图所示,对称轴为直线x=1.