题目内容
14.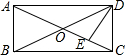 如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )| A. | 36° | B. | 9° | C. | 27° | D. | 18° |
分析 由矩形的性质得出OC=OD,得出∠ODC=∠OCD,求出∠EDC=36°,再由角的互余关系求出∠ODC,即可得出∠BDE的度数.
解答 解:∵四边形ABCD是矩形,
∴∠ADC=90°,OC=$\frac{1}{2}$AC,OD=$\frac{1}{2}$BD,AC=BD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠ADE:∠EDC=3:2,
∴∠EDC=$\frac{2}{5}$×90°=36°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠ODC=∠OCD=90°-36°=54°,
∴∠BDE=∠ODC-∠EDC=54°-36°=18°;
故选:D.
点评 本题考查了矩形的性质、等腰三角形的判定与性质、角的互余关系;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
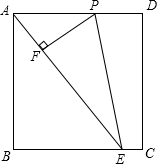 如图,矩形ABCD中,AB=4,E是BC边上一点,且BE=3,点P是射线AD上的一个动点,过点P作PF⊥AE,垂足为F,连接PE.
如图,矩形ABCD中,AB=4,E是BC边上一点,且BE=3,点P是射线AD上的一个动点,过点P作PF⊥AE,垂足为F,连接PE.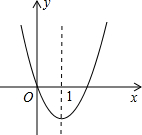 二次函数y=x2+bx的图象如图所示,对称轴为直线x=1.
二次函数y=x2+bx的图象如图所示,对称轴为直线x=1. 如图,AD是△ABC的中线,点E是AD的中点,点F是BE延长线与AC的交点,求$\frac{AF}{FC}$的值.
如图,AD是△ABC的中线,点E是AD的中点,点F是BE延长线与AC的交点,求$\frac{AF}{FC}$的值.