题目内容
15.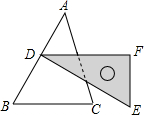 如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,且BC∥DF.若∠A=50°,则∠C的度数为70°.
如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,且BC∥DF.若∠A=50°,则∠C的度数为70°.
分析 先根据DE⊥AB得出∠ADE=90°,再由∠EDF=30°求出∠ADG的度数,根据三角形内角和定理求出∠AGD的度数,由平行线的性质即可得出结论.
解答  解:∵DE⊥AB,
解:∵DE⊥AB,
∴∠ADE=90°.
∵∠EDF=30°,
∴∠ADG=90°-30°=60°,
∵∠A=50°,
∴∠AGD=180°-60°-50°=70°.
∵∠C=∠AGD=70°.
故答案为:70°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
相关题目
10.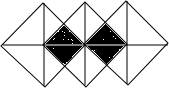 如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )
如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )
 如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )
如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
20.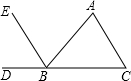 如图,能判定EB∥AC的条件是( )
如图,能判定EB∥AC的条件是( )
 如图,能判定EB∥AC的条件是( )
如图,能判定EB∥AC的条件是( )| A. | ∠C=∠ABE | B. | ∠A=∠ABE | C. | ∠C=∠ABC | D. | ∠A=∠EBD |
7.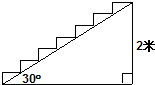 如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )
如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )
 如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )
如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )| A. | 2($\sqrt{3}$+1)m | B. | 4m | C. | ($\sqrt{3}$+2)m | D. | 2($\sqrt{3}$+3)m |
 如图,AD是△ABC的中线,点E是AD的中点,点F是BE延长线与AC的交点,求$\frac{AF}{FC}$的值.
如图,AD是△ABC的中线,点E是AD的中点,点F是BE延长线与AC的交点,求$\frac{AF}{FC}$的值.