题目内容
18.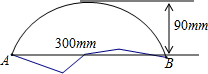 一支考古队发现一个残破的古代圆盘碎片,如图所示,考古家测量了弦AB=300mm,圆弧的高为90mm,于是得到了古圆盘的半径,从而确定了它的圆心,终于使这个古物得以复原,请问你知道考古家怎样得到它的半径吗?
一支考古队发现一个残破的古代圆盘碎片,如图所示,考古家测量了弦AB=300mm,圆弧的高为90mm,于是得到了古圆盘的半径,从而确定了它的圆心,终于使这个古物得以复原,请问你知道考古家怎样得到它的半径吗?
分析 首先在古代圆盘碎片另取点E,作出AE和AB的垂直平分线,两线交于点O即为圆心,连接BO,设BO=xmm,则MO=(x-90)mm,利用勾股定理可算出BO的长.
解答  解:如图所示:连接BO,
解:如图所示:连接BO,
∵EO垂直平分AB,
∴∠OMB=90°,MB=$\frac{1}{2}AB$,
∵AB=300mm,
∴MB=150mm,
设BO=xmm,则MO=(x-90)mm,
∵MB2+MO2=BO2,
∴1502+(x-90)2=x2,
解得:x=170.
答:古圆盘的半径是170mm.
点评 此题主要考查了垂径定理的应用,关键是正确确定圆心的位置,垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
10.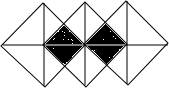 如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )
如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )
 如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )
如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
7.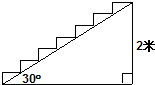 如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )
如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )
 如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )
如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )| A. | 2($\sqrt{3}$+1)m | B. | 4m | C. | ($\sqrt{3}$+2)m | D. | 2($\sqrt{3}$+3)m |
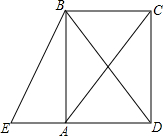 如图,四边形ABCD是矩形,延长DA至点E,使得AC=BE.
如图,四边形ABCD是矩形,延长DA至点E,使得AC=BE.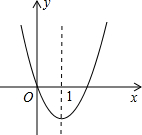 二次函数y=x2+bx的图象如图所示,对称轴为直线x=1.
二次函数y=x2+bx的图象如图所示,对称轴为直线x=1. 如图,AD是△ABC的中线,点E是AD的中点,点F是BE延长线与AC的交点,求$\frac{AF}{FC}$的值.
如图,AD是△ABC的中线,点E是AD的中点,点F是BE延长线与AC的交点,求$\frac{AF}{FC}$的值.