Question

6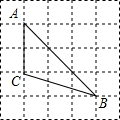．如图，方格中的每个小正方形的边长均为1，已知△ABC的三个顶点均在小正方形的顶点上，则sinB的值为（　　）

• A． $\frac{\sqrt{3}}{3}$
• B． $\frac{2\sqrt{3}}{3}$
• C． $\frac{2\sqrt{5}}{3}$
• D． $\frac{\sqrt{5}}{5}$

Answer 1

分析 连接CD，根据勾股定理及其逆定理得到∠CDB=90°，根据正弦的定义计算即可．

解答 解：连接CD，
由勾股定理得，CD=$\sqrt{2}$，BC=$\sqrt{10}$，BD=2$\sqrt{2}$，
则CD²+BD²=BC²，
∴∠CDB=90°，
∴sinB=$\frac{CD}{BC}$=$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{5}}{5}$，
故选：D．

点评 本题考查的是锐角三角函数的定义和勾股定理及其逆定理的应用，在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．．