题目内容
17.已知下列等式:①32-12=8,
②52-32=16,
③72-52=24,
…
(1)请仔细观察,写出第4个式子;
(2)根据以上式子的规律,写出第n个式子,并用所学知识说明第n个等式成立;
(3)利用(2)中发现的规律计算:8+16+24+…+792+800.
分析 (1)根据所给式子可知32-12=(2×1+1)2-(2×1-1)2=8×1;52-32=(2×2+1)2-(2×2-1)2=8×2;72-52=(2×3+1)2-(2×3-1)2=8×3;由此易得第4个式子;
(2)根据(1)的推理可得第n个式子,利用完全平方公式可证得结果;
(3)利用(2)的规律可得8+16+24+…+792+800=32-12+52-32+72-52+…+2012-1992,易得结果.
解答 解:(1)∵第1个式子为:32-12=(2×1+1)2-(2×1-1)2=8×1;
第2个式子为:52-32=(2×2+1)2-(2×2-1)2=8×2;
第3个式子为:72-52=(2×3+1)2-(2×3-1)2=8×3;
∴第4个式子为:(2×4+1)2-(2×4-1)2=92-72=32;
即第4个式子为:92-72=32;
(2)由(1)的推理过程可得,
第n个式子为:(2n+1)2-(2n-1)2=8n;
∵左边=4n2+4n+1-4n2+4n-1=8n=右边,
∴所写等式成立;
(3)8+16+24+…+792+800=32-12+52-32+72-52+…+2012-1992
=2012-1
=40400.
点评 本题主要考查了数字的变化规律,发现规律运用规律是解答此题的关键.

练习册系列答案
相关题目
5.若3x=a,3y=b,则32x+y的值为( )
| A. | a2b | B. | ab2 | C. | ab | D. | 3a2b |
9.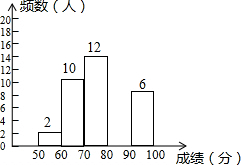 为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉子听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉子得1分,本次决赛,学生成绩为x(分),且50≤x<100(无满分),将其按分数段分为五组,绘制出以下不完整表格:
为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉子听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉子得1分,本次决赛,学生成绩为x(分),且50≤x<100(无满分),将其按分数段分为五组,绘制出以下不完整表格:
请根据表格提供的信息,解答一下问题:
(1)本次决赛共有50名学生参加;
(2)直接写出表中a=20,b=0.24;
(3)请补全右面相应的频数分布直方图;
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为52%.
 为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉子听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉子得1分,本次决赛,学生成绩为x(分),且50≤x<100(无满分),将其按分数段分为五组,绘制出以下不完整表格:
为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉子听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉子得1分,本次决赛,学生成绩为x(分),且50≤x<100(无满分),将其按分数段分为五组,绘制出以下不完整表格:| 组别 | 成绩x(分) | 频数(人数) | 频率 |
| 一 | 50≤x<60 | 2 | 0.04 |
| 二 | 60≤x<70 | 10 | 0.2 |
| 三 | 70≤x<80 | 12 | b |
| 四 | 80≤x<90 | a | 0.4 |
| 五 | 90≤x<100 | 6 | 0.12 |
(1)本次决赛共有50名学生参加;
(2)直接写出表中a=20,b=0.24;
(3)请补全右面相应的频数分布直方图;
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为52%.
6.下列式子中,正确的是( )
| A. | $\sqrt{(±3)^{2}}$=±3 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | $\sqrt{{3}^{2}}$=±3 | D. | -$\sqrt{{3}^{2}}$=-3 |
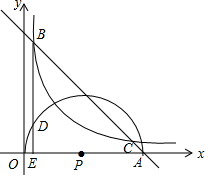 如图,已知y=-x+m(m>4)过动点A(m,0),并与反比例函数y=$\frac{4}{x}$的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=$\frac{4}{x}$的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D.
如图,已知y=-x+m(m>4)过动点A(m,0),并与反比例函数y=$\frac{4}{x}$的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=$\frac{4}{x}$的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D.
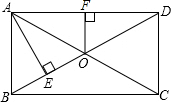 如图所示,矩形ABCD的对角线相交于点O,OF⊥AD于点F,OF=2cm,AE⊥BD于点E,且BE﹕BD=1﹕4,求AC的长.
如图所示,矩形ABCD的对角线相交于点O,OF⊥AD于点F,OF=2cm,AE⊥BD于点E,且BE﹕BD=1﹕4,求AC的长.