题目内容
2. 如图,在△ABC中,AD是高,AE是∠BAC的平分线,AF是BC边上的中线,则下列线段中,最短的是( )
如图,在△ABC中,AD是高,AE是∠BAC的平分线,AF是BC边上的中线,则下列线段中,最短的是( )| A. | AB | B. | AE | C. | AD | D. | AF |
分析 首先根据三角形的高的定义得出AD⊥BC,再根据垂线段最短求解即可.
解答 解:∵在△ABC中,AD是高,
∴AD⊥BC,
又∵在△ABC中,AE是∠BAC的平分线,AF是BC边上的中线,
∴AD<AB,AD<AE,AD<AF,
故选C.
点评 本题考查了三角形的角平分线、中线和高以及垂线段最短的性质,掌握定义与性质是解题的关键.

练习册系列答案
相关题目
14. 一个物体的三视图如下图所示,则该物体是( )
一个物体的三视图如下图所示,则该物体是( )
 一个物体的三视图如下图所示,则该物体是( )
一个物体的三视图如下图所示,则该物体是( )| A. | 圆锥 | B. | 球 | C. | 圆柱 | D. | 长方体 |
11. 如图,AB∥CD,BE平分∠ABC,∠C=36°,那么∠ABE的大小是( )
如图,AB∥CD,BE平分∠ABC,∠C=36°,那么∠ABE的大小是( )
 如图,AB∥CD,BE平分∠ABC,∠C=36°,那么∠ABE的大小是( )
如图,AB∥CD,BE平分∠ABC,∠C=36°,那么∠ABE的大小是( )| A. | 18° | B. | 24° | C. | 36° | D. | 54°. |
12.下列方程组中,为二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{\frac{1}{x}=3}\\{x-y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1=3}\\{y+2=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{xy=1}\\{3x-2y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-3y=3}\\{y=-1}\end{array}\right.$ |
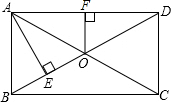 如图所示,矩形ABCD的对角线相交于点O,OF⊥AD于点F,OF=2cm,AE⊥BD于点E,且BE﹕BD=1﹕4,求AC的长.
如图所示,矩形ABCD的对角线相交于点O,OF⊥AD于点F,OF=2cm,AE⊥BD于点E,且BE﹕BD=1﹕4,求AC的长.