题目内容
7．
如图，已知抛物线y=-3（x+m）2+k与x轴交于A（1，0），B（3，0）两点，现将抛物线向左平移，记平移后的抛物线顶点为C′，当点C′恰好落在y轴上时，平移后的抛物线解析式为y=-3（x-2）2．
分析 首先求出m的值，再求出k的值，最后根据平移规律即可求出平移后的解析式．
解答 解：∵已知抛物线y=-3（x+m）2+k与x轴交于A（1，0），B（3，0）两点，
∴∴把点A，B分别代入解析式中得：-3（1+m）2+k=0，-3（3+m）2+k=0，
∴（1+m）2=（m+3）2，即1+2m=9+6m，
∴m=-2，
∴y=-3（x-2）2+k，
把A（1，0）代入y=-3（x-2）2+k，中得k=3，
∴函数解析式为：y=-3（x-2）2+3，
当y=-3（x-2）2+3向左平移2个单位，点C′恰好落在y轴上，
此时抛物线的解析式为y=-3（x-2）2，
故答案为y=-3（x-2）2．
点评 本题主要考查了抛物线与x轴的交点以及二次函数图象的几何变换，解题的关键是求出m和k的值，此题难度不大．
练习册系列答案
相关题目
17．
如图所示，一棵大树高8米，一场大风过后，大树在离地面3米处折断倒下，树的顶端落在地上，则此时树的顶端离树的底部有（ ）米．
如图所示，一棵大树高8米，一场大风过后，大树在离地面3米处折断倒下，树的顶端落在地上，则此时树的顶端离树的底部有（ ）米．| A． | 4 | B． | 3.5 | C． | 5 | D． | 13.6 |
18．下列根式中已经化简为最简形式的是（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{2{x}^{3}}$ | C． | $\sqrt{\frac{1}{3}}$ | D． | $\sqrt{{a}^{2}+{b}^{2}}$ |
把下列各数在数轴上表示出来，并用“＜”把它们连接起来．
如图，矩形ABCO中，点B的坐标为（4，2），点E为AB边上的一点，坐标为（1，2），点M为y轴负半轴上一动点，点N为x轴正半轴上一动点，且∠MEN=90°，在直线y=-10x+60上找点F，使∠BEF=∠EMN，请直接写出点F的坐标．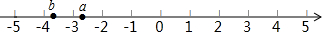
我们知道：a、b在数轴上对应的A、B两点之间距离|AB|=|a-b|
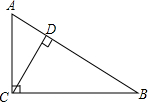如图，在Rt△ABC中，∠C=90°，CD是△ABC的高，BC=12，AC=8，AB，CD的长各是多少？