题目内容
4.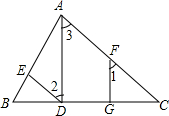 已知AD⊥BC于D,FG⊥BC垂足分别为D,G,且∠1=∠2,∠C=50°,求∠EDC的度数.
已知AD⊥BC于D,FG⊥BC垂足分别为D,G,且∠1=∠2,∠C=50°,求∠EDC的度数.证明:∵AD⊥BC,FG⊥BC,
∴∠ADC=90°,∠FGC=90°(垂直的定义).
∴AD∥FG(同位角相等,两直线平行).
∴∠1=∠3
又∵∠1=∠2,
∴∠2=∠3(等量代换).
∴DE∥AC.
∴∠EDC+∠C=180°(两直线平行,同旁内角互补).
∵∠C=50°.
∴∠EDC=130°.
分析 先根据垂直的定义得出∠ADC=90°,∠FGC=90°,故可得出AD∥FG,再由∠1=∠2可知∠2=∠3,
所以DE∥AC,根据两直线平行,同旁内角互补即可得出结论.
解答 证明:∵AD⊥BC,FG⊥BC,
∴∠ADC=90°,∠FGC=90°(垂直的定义),
∴AD∥FG(同位角相等,两直线平行),
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3(等量代换),
∴DE∥AC.
∴∠EDC+∠C=180°(两直线平行,同旁内角互补).
∵∠C=50°.
∴∠EDC=130°.
故答案为:90°,垂直的定义;AD,同位角相等,两直线平行;等量代换;AC;两直线平行,同旁内角互补;130.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
相关题目
9.根据下列条件,能判定△ABC≌△DEF的是( )
| A. | AB=DE,BC=EF,∠A=∠D | B. | ∠A=∠D,∠C=∠F,AC=DF | ||
| C. | ∠B=∠E,∠A=∠D,AC=EF | D. | AB=DE,BC=EF,∠B=∠D |
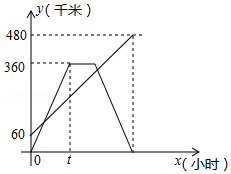 甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题: 如图,直线AB与CD相交于点O,且∠1+∠2=60°,∠AOD的度数为150°.
如图,直线AB与CD相交于点O,且∠1+∠2=60°,∠AOD的度数为150°.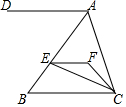 如图,EF∥AD,AD∥BC,∠DAC=120°.
如图,EF∥AD,AD∥BC,∠DAC=120°.