题目内容
14.若$\sqrt{{x^2}-6x+9}$=3-x,则x的取值范围是( )| A. | x为任意实数 | B. | x≥3 | C. | x>3 | D. | x≤3 |
分析 先依据完全平方公式对被开方数进行变形,然后依据二次根式的性质和绝对值的性质求解即可.
解答 解:∵$\sqrt{{x^2}-6x+9}$=$\sqrt{(x-3)^{2}}$=|x-3|=3-x,
∴x-3≤0.
∴x≤3.
故选:D.
点评 本题主要考查的是二次根式的性质,掌握二次根式的性质是解题的关键.

练习册系列答案
相关题目
2. 把一块直尺与一块三角板如图放置,若∠1=140°,则∠2的度数是( )
把一块直尺与一块三角板如图放置,若∠1=140°,则∠2的度数是( )
 把一块直尺与一块三角板如图放置,若∠1=140°,则∠2的度数是( )
把一块直尺与一块三角板如图放置,若∠1=140°,则∠2的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
9.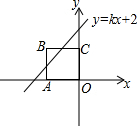 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
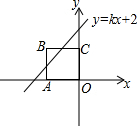 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 3 |
19.已知y是x的一次函数,表中列出了部分对应值,则m等于-2
| x | -1 | 0 | 1 |
| y | 1 | m | -5 |
6.对于函数y=-2x+1有以下四个结论,其中正确的结论是( )
| A. | 函数图象必经过点(-2,1) | B. | 函数图象经过第一、二、三象限 | ||
| C. | 函数值y随x的增大而增大 | D. | 当x>$\frac{1}{2}$,时,y<0 |
3.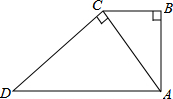 如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则
如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则
△ABC与△DCA的面积比为( )
 如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则
如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则△ABC与△DCA的面积比为( )
| A. | 2:3 | B. | 2:5 | C. | 4:9 | D. | $\sqrt{2}$:$\sqrt{3}$ |
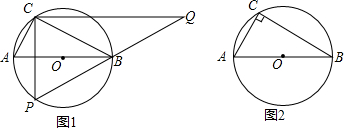 如图,AB为⊙O的直径,点C为圆上一定点,AC=6,BC=8,P为⊙O上一动点,过C作CQ⊥CP,交PB延长线于Q.
如图,AB为⊙O的直径,点C为圆上一定点,AC=6,BC=8,P为⊙O上一动点,过C作CQ⊥CP,交PB延长线于Q.