题目内容
9.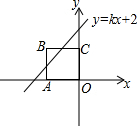 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 3 |
分析 根据正方形的性质得出点A与点B的坐标,代入解析式得出范围解答即可.
解答 解:由题意可得:点A(-1,0),点B(-1,1),
把点A代入解析式可得:-k+2=0,
解得:k=2,
把点B代入解析式可得:-k+2=1,
解得:k=1,
所以k的取值范围为:1≤k≤2,
故选B
点评 此题考查两直线相交与平行问题,关键是根据正方形的性质得出点A与点B的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列命题是假命题的是( )
| A. | 平行四边形的对角相等 | B. | 四条边都相等的四边形是菱形 | ||
| C. | 正方形的两条对角线互相垂直 | D. | 矩形的两条对角线互相垂直 |
14.若$\sqrt{{x^2}-6x+9}$=3-x,则x的取值范围是( )
| A. | x为任意实数 | B. | x≥3 | C. | x>3 | D. | x≤3 |
1. 如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=4cm2,则S△ABC为( )
如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=4cm2,则S△ABC为( )
 如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=4cm2,则S△ABC为( )
如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=4cm2,则S△ABC为( )| A. | 1cm2 | B. | 2cm2 | C. | 8cm2 | D. | 16cm2 |
18.下列说法中,正确的是( )
| A. | 在同一平面内,不相交的两条直线必平行 | |
| B. | 过任意一点可作一条已知直线的平行线 | |
| C. | 两条直线被第三条直线所截,所得到同位角相等 | |
| D. | 两条直线的交点叫做垂足 |
 如图,△ABC的三个顶点和点O都在正方形网格的格点上,每个小正方形的边长都为1.
如图,△ABC的三个顶点和点O都在正方形网格的格点上,每个小正方形的边长都为1. 如图,在直角体系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),C是y轴上的点.
如图,在直角体系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),C是y轴上的点.