题目内容
4.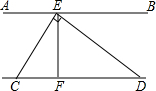 如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )
如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 先根据∠CED=90°,EF⊥CD可得出∠EDF+∠DEF=90°,∠EDF+∠DCE=90°,再由平行线的性质可知∠DCE=∠AEC,故∠AEC+∠EDF=90°,由此可得出结论.
解答 解:∵∠CED=90°,EF⊥CD,
∴∠EDF+∠DEF=90°,∠EDF+∠DCE=90°.
∵AB∥CD,
∴∠DCE=∠AEC,
∴∠AEC+∠EDF=90°.
故选B.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列说法正确的是( )
| A. | 若ab=0,则点P(a,b)表示原点 | |
| B. | 点(1,-a2)在第四象限 | |
| C. | 已知点A(2,3)与点B(2,-3),则直线AB平行x轴 | |
| D. | 坐标轴上的点不属于任何象限 |
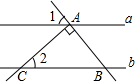 如图,直线a∥b,点A在直线a上,AB⊥AC垂足为A,若∠1=42°,则∠2为48度.
如图,直线a∥b,点A在直线a上,AB⊥AC垂足为A,若∠1=42°,则∠2为48度.