题目内容
14.方程x2+bx-6=0的根可看作y1=$\frac{6}{x}$的图象与y2=x+b的图象交点的横坐标,依此方法,若方程x2+bx-6=0的一个实数根为m,且满足2≤m<3,则满足条件的整数b的值为0或1.分析 由方程x2+bx-6=0的一个实根为m,且满足2<m<3,易求得y1=$\frac{6}{x}$的图象与y2=x+b的图象一个交点在点(2,3)与(3,2)之间,将其代入y2=x+b,即可求得b的取值范围;
解答 解:∵方程x2+bx-k=0的根可看做y1=$\frac{6}{x}$的图象与y2=x+b的图象交点的横坐标,且方程x2+bx-k=0的一个实根为m,满足2≤m<3,
∴当x=2时,y1=$\frac{6}{2}$=3,当x=3时,y1=$\frac{6}{3}$=2,
∴y1=$\frac{6}{x}$的图象与y2=x+b的图象一个交点在点(2,3)与(3,2)之间,
∵当x=2,y=3时,2+b=3,
解得:b=1,
当x=3,y=2时,3+b=2,
解得:b=-1,
∴b的取值范围为:-1<b≤1;
∴满足条件的整数b的值为:0或1,
故答案为:0或1.
点评 此题考查了反比例函数与一次函数的交点问题,待定系数法求反比例函数的解析式以及函数与方程的关系等知识.此题难度较大,注意掌握方程思想、函数思想与数形结合思想的应用.

练习册系列答案
相关题目
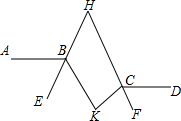 如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K-∠H=27°,则∠K=78°.
如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K-∠H=27°,则∠K=78°.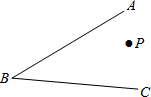 如图,P是∠ABC内一点,
如图,P是∠ABC内一点,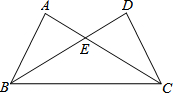 如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.