题目内容
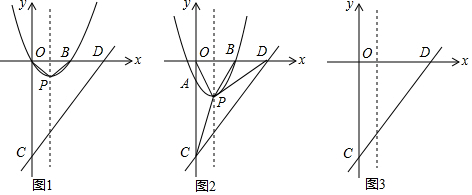
18.如图,平面直角坐标系中,抛物线y=x2-2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x-4与y轴交于点C,与x轴交于点D.(Ⅰ)直接写出点B坐标(2,0);判断△OBP的形状等腰直角三角形;
(Ⅱ)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD=$\sqrt{2}$S△POC时,求平移后的抛物线的顶点坐标;
(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.
分析 (Ⅰ)根据自变量与函数值得对应关系,可得B点坐标,根据配方法,可得顶点坐标,根据勾股定理及勾股定理的逆定理,可得答案;
(Ⅱ)根据自变量与函数值得对应关系,可得C,D,M点坐标,根据平移规律,可得P点坐标,根据平行于y轴的直线上两点间的距离较大的纵坐标减较小的纵坐标,可得PM的长,(i)根据面积的关系,可得关于m的方程,根据解方程,可得到顶点坐标;(ii)根据三角形的面积,可得答案.
解答 解:(Ⅰ)当y=0时,x2-2x=0,解得x=0(舍)或x=2,即B点坐标为(2,0),
∵抛物线y=x2-2x=(x-1)2-1,
∴P点坐标为(1,-1),由勾股定理,得
OP2=(2-1)2+12=2,
∴OP2+BP2=OB2,OP=BP,
∴△OBP是等腰直角三角形,
故答案为:(2,0),等腰直角三角形;
(Ⅱ)∵直线y=x-4与y轴交于点C,与x轴交于点D,
∴C(0,-4),D(4,0),当x=1时,y=-3,即M(1,-3),
抛物线向下平移m个单位长度,解析式为y=(x-1)2-(1+m),P(1,-1-m),
∴PM=|-(1+m)+3|=|m-2|,
S△PCD=S△PMC+S△PMD=$\frac{1}{2}$•PM•|xP-xC|=$\frac{1}{2}$•|m-2|×4=2|m-2|,
(i)S△POC=$\frac{1}{2}$•AC•|xP|=$\frac{1}{2}$×4×1=2,∵S△PCD=$\sqrt{2}$S△POC,∴S△PCD=2|m-2|=2$\sqrt{2}$,解得m=2+$\sqrt{2}$或m=2-$\sqrt{2}$,∴P(1,-3-$\sqrt{2}$)或(1,-3+$\sqrt{2}$);
(ii)S△POD=$\frac{1}{2}$OD•|yP|=$\frac{1}{2}$×4×|1-(1+m)|=2|m+1|,
①当m≥2时,S△PCD=2|m-2|=2m-4,S△POD=2|m+1|=2m+2,∴S△POD-S△PCD=6
②当-1≤m<2时,S△PCD=2|m-2=4-2m,S△POD=2|m+1|=2m+2,∴S△POD+S△PCD=6
③当m<-1时,S△PCD=2|m-2|=4-2m,S△POD=2|m+1|=2-2m,∴S△POD-S△PCD=6,
综上所述:当m≥2时,S△POD-S△PCD=6;当-1≤m<2时,S△POD+S△PCD=6;当m<-1时,S△POD-S△PCD=6.
点评 本题考查了二次函数综合题,解(Ⅰ)的关键是利用勾股定理的逆定理;解(Ⅱ)的关键是利用三角形的面积得出关于m的方程,又利用了平行于y轴的直线上两点间的距离较大的纵坐标减较小的纵坐标得出PM的长,(ii)要分类讨论,以防遗漏.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{a+3}$ | C. | $\frac{1}{a-1}$ | D. | $\frac{1}{\sqrt{a}}$ |
| A. | a≥0 | B. | a≥3 | C. | a>0 | D. | a>3 |
| A. | -30 | B. | -20 | C. | 20 | D. | 30 |
 如图,正方形ABCD中,AB=6,点E在边AB上,且BE=2AE.将△ADE沿ED对折至△FDE,延长EF交边BC于点G,连结DG,BF.下列结论:①△DCG≌△DFG;②BG=GC;③DG∥BF;④S△BFG=3.其中正确的结论是①②③(填写序号)
如图,正方形ABCD中,AB=6,点E在边AB上,且BE=2AE.将△ADE沿ED对折至△FDE,延长EF交边BC于点G,连结DG,BF.下列结论:①△DCG≌△DFG;②BG=GC;③DG∥BF;④S△BFG=3.其中正确的结论是①②③(填写序号)