已知实数a满足|2015-a|+$\sqrt{a-2016}$=a.求a-20152的值为多少? 题目和参考答案——青夏教育精英家教网—

题目内容

5．已知实数a满足|2015-a|+$\sqrt{a-2016}$=a，求a-2015²的值为多少？

分析先根据二次根式有意义的条件求出a的取值范围，再去绝对值符号，得出a=2015²-2016，代入代数式进行计算即可．

解答解：∵$\sqrt{a-2016}$有意义，
∴a-2016≥0，解得a≥2016，
∴原式=a-2015+$\sqrt{a-2016}$=a，即$\sqrt{a-2016}$=2015，解得a=2015²+2016，
∴a-2015²=2015²+2016-2015²=2016．

点评本题考查的是二次根式有意义的条件，熟知二次根式中的被开方数是非负数是解答此题的关键．

练习册系列答案

每日10分钟口算心算速算天天练系列答案

相关题目

5．

如图，在平面直角坐标系中，已知A（1，0），D（3，0），△ABC与△DEF位似，原点O是位似中心，若AB=2，则DE=6．

6．已知$\root{3}{177}$≈5.615，由此可见下面等式成立的是（　　）

A．

$\root{3}{0.177}$≈0.5615

B．

$\root{3}{0.0177}$≈0.5615

C．

$\root{3}{1.77}$≈0.5165

D．

$\root{3}{17.7}$≈56.15

13．

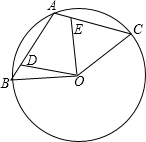已知A、B、C是圆O上的三个点，其中点A是弧BC的中点，连接AB、AC，点D、E分别在弦AB、AC上，且满足AD=CE．
求证：OD=OE．

20．如图，已知△ABC中，AC=BC，点D、E、F分别是线段AC、BC、AD的中点，BF、ED的延长线交于点G，连接GC．
（1）求证：AB=GD；
（2）如图2，当CG=EG时，求$\frac{AC}{AB}$的值．

10．分数指数幂是一个数的指数为分数，整数指数幂的运算性质也同样可以推广到分数指数幂，例如：（4${\;}^{\frac{1}{2}}$）²=4${\;}^{{\frac{1}{2}}^{{x}^{{2}^{\;}}}}$=4¹=4，则4${\;}^{\frac{1}{2}}$=2，仿照以上计算过程求8${\;}^{\frac{1}{3}}$的值为（　　）

17．

画图并填空：如图，方格纸中每个小正方形的边长都为1，在方格纸中将△ABC经过一次平移后得到△A′B′C′，图中标出来点A，点B′、点C和它的对应点C′．
（1）请画出平移前后的△ABC和△A′B′C′；
（2）利用网格画出△ABC中BC边上的中线AD；
（3）利用网格画出△ABC中AB边上的高CE；
（4）△A′B′C′的面积为6．

15．如果代数式x²+kx+49能分解成（x-7）²形式，那么k的值为（　　）

试题分类