题目内容
20.如图,已知△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,BF、ED的延长线交于点G,连接GC.(1)求证:AB=GD;
(2)如图2,当CG=EG时,求$\frac{AC}{AB}$的值.

分析 (1)由题意可知DE是△ABC的中位线,从而可知EG∥AB,又点F为线段AD的中点,所以AF=DF,然后证明△ABF≌△DGF即可求证AB=GD.
(2)由条件可知DE=$\frac{1}{2}$AB,EG=$\frac{3}{2}$AB,然后利用DE∥AB,证明△GEC∽△CBA,从而求出$\frac{AC}{AB}$的值.
解答 解:(1)∵D、E分别是线段AC、BC的中点,
∴DE为△ABC的中位线,
∴DE∥AB,即EG∥AB,
∴∠FDG=∠A,
∵点F为线段AD的中点,
∴AF=DF,
在△ABF与△DGF中,
$\left\{\begin{array}{l}{∠A=∠FDG}\\{AF=DF}\\{∠AFB=∠DFG}\end{array}\right.$
∴△ABF≌△DGF(ASA)
∴AB=GD
(2)∵DE为△ABC的中位线,
∴DE=$\frac{1}{2}$AB,CE=$\frac{1}{2}$BC=$\frac{1}{2}$AC
∵DG=AB,
∴EG=DE+DG
∴EG=$\frac{3}{2}$AB
∵DE∥AB,
∴∠GEC=∠CBA,
∵AC=BC,CG=EG
∴△GEC∽△CBA
∴$\frac{CE}{AB}=\frac{CG}{AC}=\frac{EG}{AC}$,
即$\frac{\frac{1}{2}AC}{AB}=\frac{\frac{3}{2}AB}{AC}$,
∴$\frac{AC}{AB}=\sqrt{3}$
点评 本题考查相似三角形的综合问题,涉及全等三角形的性质与判定,相似三角形的性质与判断,中位线的性质,综合程度较高,属于中等题型.

练习册系列答案
相关题目
1.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (-2xy2)3=-8x3y5 | C. | 2a-3=$\frac{1}{2{a}^{3}}$ | D. | (-a)3÷(2a)2=-$\frac{1}{4}$a |
8.已知在△ABC中,AB=14,BC=13,tanB=$\frac{12}{5}$,则sinA的值为( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{7}{25}$ | D. | $\frac{56}{65}$ |
15.圣诞节将至,小华决定购买一些贺卡,贺卡店有一则广告如图:
(1)如果小华只买15张,则购买贺卡共花去多少元钱?
(2)如果小华购买x张,请用含x的代数式表示小华所花的费用;
(3)如果小华此次购买共花去360元,请问购买贺卡可能多少张?
| 购买贺卡须知 (a)若购买20张以内(含20张),每张贺卡20元; (b)若购买20张以上,所购贺卡按照价格全部打七五折. |
(2)如果小华购买x张,请用含x的代数式表示小华所花的费用;
(3)如果小华此次购买共花去360元,请问购买贺卡可能多少张?

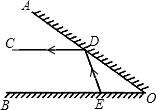 如图,∠AOB的两边OA、OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,光线经过镜子反射时,∠ADC=∠ODE,∠DEB=70°.
如图,∠AOB的两边OA、OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,光线经过镜子反射时,∠ADC=∠ODE,∠DEB=70°.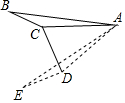 如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子α+β=180°.
如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子α+β=180°.