题目内容
14.已知一元二次方程2x2+x+k=0无实数根,那么反比例函数y=$\frac{k}{x}$的图象位于( )| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一象限 | D. | 无法确定 |
分析 由关于x的一元二次方程2x2+x+k=0无实数根,所以△<0,求出k的取值范围,进而根据反比例函数的性质求解即可.
解答 解:∵一元二次方程2x2+x+k=0无实数根,
∴△<0,即△=12-4×2k=1-8k<0,
解得:k>$\frac{1}{8}$
∴k>0,
∴反比例函数y=$\frac{k}{x}$的图象位于第一、三象限.
故选A.
点评 此题考查了根的判别式.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.同时考查了反比例函数的性质.

练习册系列答案
相关题目
4.在△ABC中,AC=6,BC=8,AB=10,则点C到AB边的距离是( )
| A. | $\frac{24}{5}$ | B. | $\frac{5}{24}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
5.礼堂第一排有m个座位,后面每排比前一排多一个座位,则第n排的座位个数有( )
| A. | m+n | B. | mn+1 | C. | m+(n-1) | D. | n+(n+1) |
2.1微米=0.000001米,1微米用科学记数法可表示为( )米.
| A. | 1×106 | B. | 1×105 | C. | 1×10-5 | D. | 1×10-6 |
3.已知等式3a=5b-1,则下列等式中不一定成立的是( )
| A. | 3a-3=5b-4 | B. | 3a+b=6b-1 | C. | 3ac=5bc-1 | D. | b=$\frac{3a+1}{5}$ |
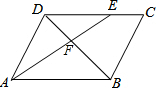 如图,在?ABCD中,AB=6,AD=4,∠BAD的平分线AE分别交BD、CD于F、E,那么$\frac{DF}{BF}$=$\frac{2}{3}$.
如图,在?ABCD中,AB=6,AD=4,∠BAD的平分线AE分别交BD、CD于F、E,那么$\frac{DF}{BF}$=$\frac{2}{3}$.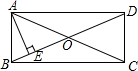 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作BD的垂线,垂足为E,若∠EAD=3∠BAE,则∠AOE=45°.
如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作BD的垂线,垂足为E,若∠EAD=3∠BAE,则∠AOE=45°. 如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为8.
如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为8.