题目内容
17.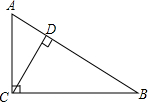 如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD=$\frac{36}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD=$\frac{36}{5}$.
分析 首先根据勾股定理求出斜边AB的长,再根据三角形的面积为定值即可求出点C到AB的距离.
解答 解:在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,
∵BC=12,AC=9,
∴AB=$\sqrt{{AC}^{2}+B{C}^{2}}$=$\sqrt{{9}^{2}+1{2}^{2}}$=15,
∵△ABC的面积=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
∴CD=$\frac{AC×BC}{AB}$=$\frac{9×12}{15}$=$\frac{36}{5}$,
故答案为:$\frac{36}{5}$.
点评 本题考查了勾股定理、三角形面积的计算方法;熟练掌握勾股定理,通过三角形面积求出CD是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.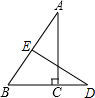 如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3cm,AB的垂直平分线DE交BC的延长线于点D,则CD的长为( )
如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3cm,AB的垂直平分线DE交BC的延长线于点D,则CD的长为( )
 如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3cm,AB的垂直平分线DE交BC的延长线于点D,则CD的长为( )
如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3cm,AB的垂直平分线DE交BC的延长线于点D,则CD的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
8.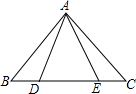 如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
 如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )| A. | △ABD和△ACE成轴对称 | B. | △ABD和△ACE成中心对称 | ||
| C. | △ABD经过旋转可以和△ACE重合 | D. | △ABD经过平移可以和△ACE重合 |
5.礼堂第一排有m个座位,后面每排比前一排多一个座位,则第n排的座位个数有( )
| A. | m+n | B. | mn+1 | C. | m+(n-1) | D. | n+(n+1) |
2.1微米=0.000001米,1微米用科学记数法可表示为( )米.
| A. | 1×106 | B. | 1×105 | C. | 1×10-5 | D. | 1×10-6 |
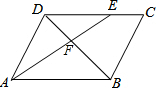 如图,在?ABCD中,AB=6,AD=4,∠BAD的平分线AE分别交BD、CD于F、E,那么$\frac{DF}{BF}$=$\frac{2}{3}$.
如图,在?ABCD中,AB=6,AD=4,∠BAD的平分线AE分别交BD、CD于F、E,那么$\frac{DF}{BF}$=$\frac{2}{3}$.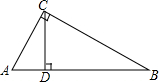 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值.