题目内容
7.先化简,再求值.($\frac{8}{x+1}$-x+1)÷$\frac{{x}^{2}+6x+9}{x+1}$,其中x的取值-3$\sqrt{2}$,-4,-$\sqrt{17}$,-(2$\sqrt{5}$-1)这四个实数中最小值.分析 先将括号内通分,然后因式分解,再约分.
解答 解:原式=[$\frac{8}{x+1}$-$\frac{{x}^{2}-1}{x+1}$]•$\frac{x+1}{(x+3)^{2}}$
=$\frac{9-{x}^{2}}{x+1}$•$\frac{x+1}{(x+3)^{2}}$
=$\frac{(3-x)(3+x)}{x+1}$•$\frac{x+1}{(x+3)^{2}}$
=$\frac{3-x}{x+3}$;
∵-3$\sqrt{2}$=-$\sqrt{18}$,-4=-$\sqrt{16}$,-$\sqrt{17}$,-(2$\sqrt{5}$-1)=-$\sqrt{20}$+1,
∴-3$\sqrt{2}$最小,
当x=-3$\sqrt{2}$时,原式=$\frac{3+3\sqrt{2}}{-3\sqrt{2}+3}$=$\frac{1+\sqrt{2}}{1-\sqrt{2}}$=$\frac{(1+\sqrt{2})^{2}}{1-2}$=-(1+$\sqrt{2}$)2.
点评 本题考查了分式的化简求值,熟悉约分、通分、因式分解是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
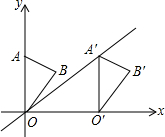 如图,在平面直角坐标系中,点A,B的坐标分别为(0,4)和(1,3)△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′在直线y=$\frac{4}{5}$x上,则点B与O′间的距离为( )
如图,在平面直角坐标系中,点A,B的坐标分别为(0,4)和(1,3)△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′在直线y=$\frac{4}{5}$x上,则点B与O′间的距离为( ) 如图,AB是⊙O的直径,且AB=2cm,点P为弧AB上一动点(不与A,B重合),$\widehat{AD}$=$\widehat{BD}$,过点D作⊙O的切线交PB的延长线于点C.
如图,AB是⊙O的直径,且AB=2cm,点P为弧AB上一动点(不与A,B重合),$\widehat{AD}$=$\widehat{BD}$,过点D作⊙O的切线交PB的延长线于点C.