题目内容
1.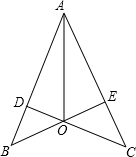 如图,OA平分∠BAC,∠AOD=∠AOE,则图中的全等三角形共有3对.
如图,OA平分∠BAC,∠AOD=∠AOE,则图中的全等三角形共有3对.
分析 根据给定的条件以及角平分线的定义,利用全等三角形的判定定理ASA即可证出△DAO≌△EAO,再根据全等三角形的性质找出相等的边角关系,利用全等三角形的判定定理即可得出△BDO≌△CEO(ASA)和△AOB≌△AOC(SAS),此题的解.
解答 解:∵OA平分∠BAC,
∴∠DAO=∠EAO.
在△DAO和△EAO中,$\left\{\begin{array}{l}{∠DAO=∠EAO}\\{AO=AO}\\{∠AOD=∠AOE}\end{array}\right.$,
∴△DAO≌△EAO(ASA).
∴OD=OE,∠ADO=∠AEO,
∴∠BDO=∠CEO.
在△BDO和△CEO中,$\left\{\begin{array}{l}{∠BDO=∠CEO}\\{OD=OE}\\{∠BOD=∠COE}\end{array}\right.$,
∴△BDO≌△CEO(ASA),
∴OB=OC.
∵∠AOD=∠AOE,∠BOD=∠COE,
∴∠AOB=∠AOC.
在△AOB和△AOC中,$\left\{\begin{array}{l}{AO=AO}\\{∠AOB=∠AOC}\\{OB=OC}\end{array}\right.$,
∴△AOB≌△AOC(SAS).
故答案为:3.
点评 本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定定理以及性质定理是解题的关键.

练习册系列答案
相关题目
6.如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成如图图案,则第8个图案中有n个白色纸片,则n的值为( )


| A. | 23 | B. | 24 | C. | 25 | D. | 26 |
13.将方程-5x2=2x+10化为二次项系数为1的一般形式是( )
| A. | x2+$\frac{2}{5}$x+2=0 | B. | x2-$\frac{2}{5}$x-2=0 | C. | x2+$\frac{2}{5}$x+10=0 | D. | x2-2x-10=0 |
 如图,直线a∥b∥c,点B是线段AC的中点,若DE=2,则EF=2.
如图,直线a∥b∥c,点B是线段AC的中点,若DE=2,则EF=2. 如图:已知y=ax2+bx+c与x轴交于A,B两点,A,B坐标分别是(-1,0)和(3,0)与y轴交于点C(0,3).
如图:已知y=ax2+bx+c与x轴交于A,B两点,A,B坐标分别是(-1,0)和(3,0)与y轴交于点C(0,3).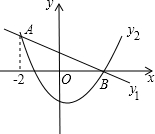 直线y1=kx+m与抛物线y2=ax2+bx+c在同一坐标中的图象如图所示,直线与抛物线相交于A(-2,2)、B(3,0),当x取值范围是-2<x<3时,y1>y2.
直线y1=kx+m与抛物线y2=ax2+bx+c在同一坐标中的图象如图所示,直线与抛物线相交于A(-2,2)、B(3,0),当x取值范围是-2<x<3时,y1>y2.