题目内容
12. 如图:已知y=ax2+bx+c与x轴交于A,B两点,A,B坐标分别是(-1,0)和(3,0)与y轴交于点C(0,3).
如图:已知y=ax2+bx+c与x轴交于A,B两点,A,B坐标分别是(-1,0)和(3,0)与y轴交于点C(0,3).(1)求抛物线解析式,并确定其对称轴;
(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得
△PDC是等腰三角形?若存在,求符合条件的点P的坐标;若不存在,请说明理由.
分析 (1)根据待定系数法求二次函数的解析式,并利用配方法求对称轴;
(2)分两种情况:①当以CD为底边时,如图2,根据两点间距离公式PD=PC,列式计算,并根据点P在对称轴右侧,所以x应该大于1进行取舍;
②当DC为腰时,如图3,则P、C关于直线x=1对称,写出点P的坐标.
解答  解:(1)如图1,把(-1,0)和(3,0)与y轴交于点C(0,3)代入y=ax2+bx+c中得:
解:(1)如图1,把(-1,0)和(3,0)与y轴交于点C(0,3)代入y=ax2+bx+c中得:
$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$,
∴抛物线解析式为:y=-x2+2x+3,
y=-x2+2x+3=-(x2-2x+1-1)+3=-(x-1)2+4,
∴对称轴是直线x=1;
(2)存在,
由(1)得D(1,4),
当△PDC是等腰三角形时,分两种情况:
①当以CD为底边时,如图2,PD=PC,
设P(x,y),
则(x-1)2+(y-4)2=x2+(y-3)2,
解得:x+y=4,
∵P在抛物线上,
∴$\left\{\begin{array}{l}{x+y=4}\\{y=-{x}^{2}+2x+3}\end{array}\right.$,
4-x=-x2+2x+3,
x1=$\frac{3+\sqrt{5}}{2}$,x2=$\frac{3-\sqrt{5}}{2}$<1(舍),
∴y=4-x=4-$\frac{3+\sqrt{5}}{2}$=$\frac{5-\sqrt{5}}{2}$,
∴P($\frac{3+\sqrt{5}}{2}$,$\frac{5-\sqrt{5}}{2}$),
②当DC为腰时,如图3,则P、C关于直线x=1对称,
∴P(2,3),
综上所述,点P的坐标为P($\frac{3+\sqrt{5}}{2}$,$\frac{5-\sqrt{5}}{2}$)或(2,3).
点评 本题是二次函数的综合问题,考查了利用待定系数法求二次函数的解析式,同时根据等腰三角形的判定分两种情况进行讨论;根据两点间距离公式列方程求解.

 阅读快车系列答案
阅读快车系列答案| A. | (2,-l) | B. | (1,-2) | C. | (-2,-l) | D. | (-2,1) |
| A. | x2=0 | B. | $\frac{1}{{{x^2}+2x}}$=0 | C. | x3-2x2+x-1=0 | D. | x2+2xy+2=0 |
 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.
在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.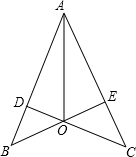 如图,OA平分∠BAC,∠AOD=∠AOE,则图中的全等三角形共有3对.
如图,OA平分∠BAC,∠AOD=∠AOE,则图中的全等三角形共有3对.