题目内容
13.解方程组:$\left\{\begin{array}{l}{ab=3\sqrt{3}}\\{tan30°=\frac{b}{a}}\end{array}\right.$.分析 由tan30°=$\frac{\sqrt{3}}{3}$=$\frac{b}{a}$,得出b=$\frac{\sqrt{3}}{3}$a,代入ab=3$\sqrt{3}$求得a,进一步求得b即可.
解答 解:$\left\{\begin{array}{l}{ab=3\sqrt{3}}\\{tan30°=\frac{b}{a}}\end{array}\right.$,
由②得tan30°=$\frac{\sqrt{3}}{3}$=$\frac{b}{a}$,b=$\frac{\sqrt{3}}{3}$a,
代入①得$\frac{\sqrt{3}}{3}$a2=3$\sqrt{3}$,
解得a=±3,
则b=±$\sqrt{3}$,
所以原方程组的解是$\left\{\begin{array}{l}{a=3}\\{b=\sqrt{3}}\end{array}\right.$或$\left\{\begin{array}{l}{a=-3}\\{b=-\sqrt{3}}\end{array}\right.$.
点评 此题考查二次根式的运用,二元二次方程组的解法以及特殊角的三角函数,解答注意符号的对应.

练习册系列答案
相关题目
5.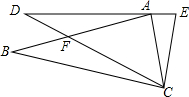 如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )
如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )
 如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )
如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )| A. | DC | B. | BC | C. | AB | D. | AE+AC |
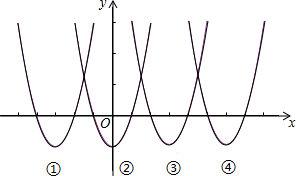 如图为函数:y=x2-1,y=x2+6x+8,y=x2-6x+8,y=x2-12x+35在同一平面直角坐标系中的图象,其中最有可能是y=x2-6x+8的图象的序号是第三个.
如图为函数:y=x2-1,y=x2+6x+8,y=x2-6x+8,y=x2-12x+35在同一平面直角坐标系中的图象,其中最有可能是y=x2-6x+8的图象的序号是第三个.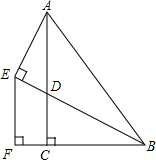 如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,连接BD,过A作AE⊥BD交BD的延长线于E,过E作EF⊥BC交BC的延长线于F,且AC=BF,BE=2AE.
如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,连接BD,过A作AE⊥BD交BD的延长线于E,过E作EF⊥BC交BC的延长线于F,且AC=BF,BE=2AE.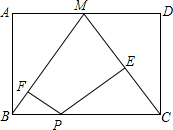 如图,点M是矩形ABCD的边AD的中点,点P是BC边上的一个动点,PE⊥CM,PF⊥BM,垂足分别E,F.
如图,点M是矩形ABCD的边AD的中点,点P是BC边上的一个动点,PE⊥CM,PF⊥BM,垂足分别E,F. 如图,电路图上有四个开关A、B、C、D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是$\frac{1}{2}$.
如图,电路图上有四个开关A、B、C、D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是$\frac{1}{2}$.