题目内容
1.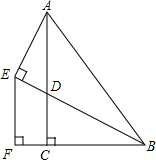 如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,连接BD,过A作AE⊥BD交BD的延长线于E,过E作EF⊥BC交BC的延长线于F,且AC=BF,BE=2AE.
如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,连接BD,过A作AE⊥BD交BD的延长线于E,过E作EF⊥BC交BC的延长线于F,且AC=BF,BE=2AE.(1)若EF=$\frac{4}{5}\sqrt{5}$,FB=$\frac{8}{5}\sqrt{5}$,AE=2,求四边形AEFB的面积;
(2)求证:BE平分∠ABC.
分析 (1)由三角形的面积和求得四边形的面积.
(2)延长AE交BF的延长线于点G,构造全等三角形,根据全等三角形的性质得到AG=BE,证得BE垂直平分AG,再由等腰三角形的性质三线合一得到结果.
解答 解:(1)∵BE=2AE,AE=2,
∴BE=4,
∴S四边形AEFB=S△AEB+S△FBE=$\frac{1}{2}$×2×4$+\frac{1}{2}$×$\frac{4\sqrt{5}}{5}$×$\frac{8\sqrt{5}}{5}$=$\frac{36}{5}$;
(2)延长AE交BF的延长线于点G,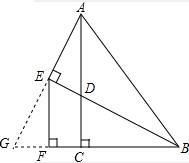
∵AE⊥BE,AC⊥BC,∠ADE=∠BDC,
∴∠EAD=∠DBC,
在△AGC与△BEF中,$\left\{\begin{array}{l}{∠ACG=∠BFE}\\{∠GAC=∠EBF}\\{AC=BF}\end{array}\right.$,
∴△AGC≌△BEF,
∴AG=BE,
∵BE=2AE,
∴AG=2AE,
∴BE垂直平分AG,
∴AB=BG,
∴BE平分∠ABC.
点评 本题考查了垂直的定义,三角形的面积的求法,全等三角形的判定与性质,线段的垂直平分线的性质,等腰三角形的性质,作辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目
11.计算:-1-2=( )
| A. | 1 | B. | -1 | C. | -2 | D. | -3 |
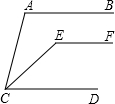 已知:如图AB∥CD,EF∥CD,CE平分∠ACD,∠A=110°,则∠CEF=145°.
已知:如图AB∥CD,EF∥CD,CE平分∠ACD,∠A=110°,则∠CEF=145°.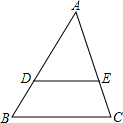 在△ABC中,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9.
在△ABC中,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9.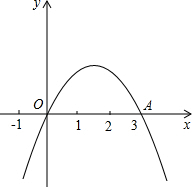 如图,二次函数y=ax2+bx+c(a≠0)的图象过原点O与点A(3,0).
如图,二次函数y=ax2+bx+c(a≠0)的图象过原点O与点A(3,0).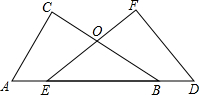 如图,已知AC⊥BC,DF⊥EF,BC 与EF交于O,AC=DF,AE=BD
如图,已知AC⊥BC,DF⊥EF,BC 与EF交于O,AC=DF,AE=BD