题目内容
4.已知菱形ABCD中,对角线AC=16,BD=12,则此菱形的高等于$\frac{48}{5}$.分析 过D作DE⊥AB于E,根据菱形的性质得出AO=$\frac{1}{2}$AC=8,DO=$\frac{1}{2}$BD=6,AC⊥BD,根据勾股定理求出AD,根据三角形面积公式求出DE即可.
解答 解:过D作DE⊥AB于E,
∵菱形ABCD中,对角线AC=16,BD=12,
∴AO=$\frac{1}{2}$AC=8,DO=$\frac{1}{2}$BD=6,AC⊥BD,
∴∠DOA=90°,
由勾股定理得:AD=$\sqrt{D{O}^{2}+A{O}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵四边形ABCD是菱形,
∴AB=AD=10,
∴S菱形ABCD=$\frac{1}{2}×AC×BD$=AB×DE,
$\frac{1}{2}$×16×12=10×DE,
∴DE=$\frac{48}{5}$,
故答案为:$\frac{48}{5}$.
点评 本题考查了菱形的性质和勾股定理的应用,能熟记菱形的性质是解此题的关键,注意:菱形的四条边都相等,菱形的对角线互相平分且垂直.

练习册系列答案
相关题目
1.绝对值最小的有理数是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 不存在 |
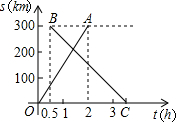 在甲、乙两城市之间每隔1小时有一列速度相同的动车组列车从甲城开往乙城.如图所示,OA是第一列动车组列车离开甲城的路程s(千米)与运行时间t(时)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(千米)与运行时间t(时)的函数图象.请根据图中信息,解答下列问题:
在甲、乙两城市之间每隔1小时有一列速度相同的动车组列车从甲城开往乙城.如图所示,OA是第一列动车组列车离开甲城的路程s(千米)与运行时间t(时)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(千米)与运行时间t(时)的函数图象.请根据图中信息,解答下列问题: 如图所示,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕A点逆时针旋转到△AB′C′的位置,使CC′∥AB,则∠BAB′=40°.
如图所示,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕A点逆时针旋转到△AB′C′的位置,使CC′∥AB,则∠BAB′=40°. 如图,在△ABC中,AB=AC,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF为⊙O的切线,交AC于点F.
如图,在△ABC中,AB=AC,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF为⊙O的切线,交AC于点F.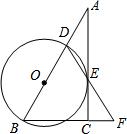 在△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC有公共点E,连结DE并延长,与BC的延长线交于点F,BD=BF.
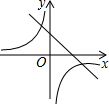
在△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC有公共点E,连结DE并延长,与BC的延长线交于点F,BD=BF. 已知:抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则一次函数y=ax+b(a≠0)与反比例函数y=$\frac{c}{x}$在同一直角坐标系中的图象大致是( )
已知:抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则一次函数y=ax+b(a≠0)与反比例函数y=$\frac{c}{x}$在同一直角坐标系中的图象大致是( )