题目内容
7.今年“五一”小黄金周期间,我市旅游公司组织50名游客分散到A、B、C三个景点游玩.三个景点的门票价格如表所示:| 景点 | A | B | C |
| 门票单价(元) | 30 | 55 | 75 |
(1)写出y与x之间的函数关系式;
(2)设购买门票总费用为w(元),求出w与x之间的函数关系式;
(3)若每种票至少购买1张,且A种票不少于10张,则共有几种购票方案?并求出购票总费用最少时,购买A、B、C三种票的张数.
分析 (1)根据A,B之间的数量关系,利用A种+B种+C种=50求出y与x的函数关系即可;
(2)根据A,B,C三种门票的价格以及张数得出总费用即可;
(3)根据每种票至少购买一张,且A种票不少于10张,得出不等式组,求出x的取值范围,进而得出购票方案即可.
解答 解:(1)∵欲购买的50张票中,B种票张数是A种票张数的3后还多1张
设需购A种票张数为x,C种票张数为y,
∴x+3x+1+y=50,
整理得出:y=-4x+49;
(2)根据三种门票的单价可得W=30x+55(3x+1)+75(-4x+49)=-105x+3730;
(3)由题意得出$\left\{\begin{array}{l}{x≥10}\\{3x+1≥1}\\{-4x+49≥1}\end{array}\right.$,
解得:10≤x≤12,
故共有3种购票方案,即A种10张,B种31张,C种9张,
此时总费用为30×10+55×31+75×9=2680元
A种11张,B种34张,C种5张;
此时总费用为30×11+55×34+75×5=2575元
A种12张,B种37张,C种1张;
此时总费用为30×12+55×37+75×1=2470元(或根据A种票价最低,即购买A种门票越多,费用越低)
故购票费用最少时,购买A种票12张,B种票37张,C种票1张
点评 此题主要考查了一次函数的应用以及不等式组的应用等知识,根据已知得出x的取值范围是解题关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
19.下列各组数中,不能作为直角三角形边长的是( )
| A. | 9,12,15 | B. | 5,12,13 | C. | 1,2,$\sqrt{3}$ | D. | ,3,5,7 |
16.由方程组$\left\{\begin{array}{l}{2x+m=1}\\{y-3=m}\end{array}\right.$,可得x与y的关系是( )
| A. | 2x+y=-4 | B. | 2x-y=-4 | C. | 2x+y=4 | D. | 2x-y=4 |

 如图,在△AOC中,OA=OC,点B是AO延长线上一点,OD平分∠AOC交AC于点D,OM平分∠COB,CF⊥OM于点F.
如图,在△AOC中,OA=OC,点B是AO延长线上一点,OD平分∠AOC交AC于点D,OM平分∠COB,CF⊥OM于点F. (1)如图,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度数.
(1)如图,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度数.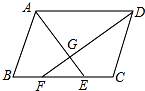 如图,在?ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.
如图,在?ABCD中,∠BAD、∠ADC的平分线AE、DF分别交BC于点E、F,AE与DF相交于点G.