题目内容
5.根据图1的程序,得到了y与x的函数图象,如图2,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ,则下列结论:①x<0时,y=$\frac{2}{x}$;②△OPQ的面积为定值;③x>0时,y随x的增大而增大;④MQ=2PM;⑤∠POQ可以等于90°.其中正确的有( )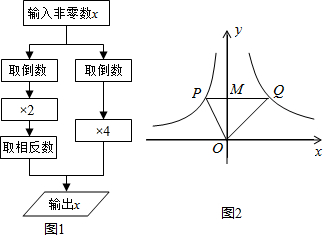
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据题意得到当x<0时,y=-$\frac{2}{x}$,当x>0时,y=$\frac{4}{x}$,设P(a,b),Q(c,d),求出ab=-2,cd=4,求出△OPQ的面积是3;x>0时,y随x的增大而减小;由ab=-2,cd=4得到MQ=2PM;因为∠POQ=90°也行,根据结论即可判断答案.
解答 解:①、x<0,y=-$\frac{2}{x}$,∴故此选项①错误;
②、当x<0时,y=-$\frac{2}{x}$,当x>0时,y=$\frac{4}{x}$,
设P(a,b),Q(c,d),
则ab=-2,cd=4,
∴△OPQ的面积是$\frac{1}{2}$(-a)b+$\frac{1}{2}$cd=3,∴故此选项②正确;
③、x>0时,y=$\frac{4}{x}$=4•$\frac{1}{x}$,y随x的增大而减小,故此选项③错误;
④、∵ab=-2,cd=4,∴故此选项④正确;
⑤设PM=-a,则OM=-$\frac{2}{a}$.则P02=PM2+OM2=(-a)2+(-$\frac{2}{a}$)2=(-a)2+$\frac{4}{{a}^{2}}$,
QO2=MQ2+OM2=(-2a)2+(-$\frac{2}{a}$)2=4a2+$\frac{4}{{a}^{2}}$,
当PQ2=PO2+QO2=(-a)2+$\frac{4}{{a}^{2}}$+4a2+$\frac{4}{{a}^{2}}$=5a2+$\frac{8}{{a}^{2}}$=9a2
整理得:$\frac{8}{{a}^{2}}$=4a2
∴a4=2,
∵a有解,
∴∠POQ=90°可能存在,故此选项⑤正确;
正确的有②④⑤,
故答案为:②④⑤.
点评 本题主要考查对反比例函数的性质,反比例函数图象上点的坐标特征,三角形的面积等知识点的理解和掌握,能根据这些性质进行说理是解此题的关键.

 名校课堂系列答案
名校课堂系列答案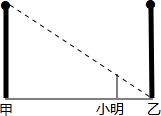 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )| A. | 7米 | B. | 8米 | C. | 9米 | D. | 10米 |
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )| A. | 10 | B. | 17 | C. | 20 | D. | 21.5 |
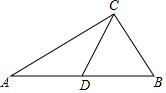 如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )
如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )| A. | $\frac{\sqrt{17}-1}{2}$ | B. | 2 | C. | 4$\sqrt{2}$-4 | D. | $\frac{4}{3}$$\sqrt{3}$ |
| A. | $\left\{{\begin{array}{l}{k=-1}\\{b=1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{k=-1}\\{b=0}\end{array}}\right.$ | C. | $\left\{\begin{array}{l}k=1\\ b=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}k=1\\ b=-4\end{array}\right.$ |
| A. | 60(x+30)+90x=480 | B. | 60x+90(x+30)=480 | ||
| C. | 60(x+$\frac{30}{60}$)+90x=480 | D. | 60x+90(x+$\frac{30}{60}$)=480 |
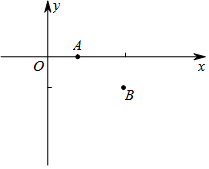 如图,已知平面直角坐标系中,点A的坐标是(1,0),点B的坐标是(3,-1),C是坐标轴上的点,使得△ABC为直角三角形,则点C的坐标为(3,0)或($\frac{7}{2}$,0)或(0,-7)或(0,-2).
如图,已知平面直角坐标系中,点A的坐标是(1,0),点B的坐标是(3,-1),C是坐标轴上的点,使得△ABC为直角三角形,则点C的坐标为(3,0)或($\frac{7}{2}$,0)或(0,-7)或(0,-2).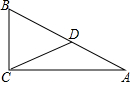 如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=5.
如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=5.