题目内容
15.A、B两地相距480千米,一列慢车从A地出发,每小时行驶60千米,一列快车从B地出发,每小时行驶90千米,快车提前30分钟出发,两车相向而行,慢车行驶多少小时后两车相遇?设慢车行驶x小时后两车相遇,根据题意,下面所列方程正确的是( )| A. | 60(x+30)+90x=480 | B. | 60x+90(x+30)=480 | ||
| C. | 60(x+$\frac{30}{60}$)+90x=480 | D. | 60x+90(x+$\frac{30}{60}$)=480 |
分析 根据题意可以找出题目中的等量关系,列出相应的方程,从而可以解答本题.
解答 解:由题意可得,
60x+90(x+$\frac{30}{60}$)=480,
故选D.
点评 本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,列出相应的方程.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
3.为了解某市参加中考的40073名学生的身高情况,抽查了其中1000名学生的身高进行统计分析.下面叙述正确的是( )
| A. | 40073名学生是总体 | |
| B. | 每名学生是总体的一个个体 | |
| C. | 本次调查是全面调查 | |
| D. | 1000名学生的身高是总体的一个样本 |
10. 问题情境
问题情境
已知矩形的面积为S(S为常数,S>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+$\frac{S}{x}$)(x>0)
探索研究
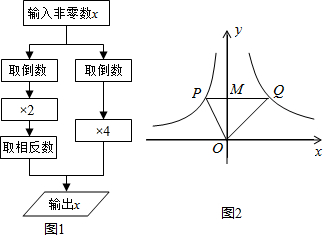
我们可以借鉴学习函数的经验,先探索函数y=x+$\frac{1}{x}$(x>0)的图象性质.
①列表:
表中m=$\frac{10}{3}$;
②描点:如图所示;
③连线:请在图中画出该函数的图象;
④观察图象,写出两条函数的性质;函数有最小值2;当x>1时,y随x的增大而增大
解决问题
在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.同样通过配方也可以求函数y=x+$\frac{1}{x}$(x>0)的最小值.
y=x+$\frac{1}{x}$=${(\sqrt{x})}^{2}$+${(\sqrt{\frac{1}{x}})}^{2}$=${(\sqrt{x})}^{2}$+${(\sqrt{\frac{1}{x}})}^{2}$-2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$+2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$=${(\sqrt{x}-\sqrt{\frac{1}{x})}}^{2}$+2
∵${({\sqrt{x}-\sqrt{\frac{1}{x}}})^2}$≥0,∴y≥2
∴当$\sqrt{x}$-$\sqrt{\frac{1}{x}}$=0,即x=1时,y最小值=2
请类比上面配方法,直接写出“问题情境”中的问题答案.
 问题情境
问题情境已知矩形的面积为S(S为常数,S>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+$\frac{S}{x}$)(x>0)
探索研究
我们可以借鉴学习函数的经验,先探索函数y=x+$\frac{1}{x}$(x>0)的图象性质.
①列表:
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{4}$ | m | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | $\frac{17}{4}$ | … |
②描点:如图所示;
③连线:请在图中画出该函数的图象;
④观察图象,写出两条函数的性质;函数有最小值2;当x>1时,y随x的增大而增大
解决问题
在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.同样通过配方也可以求函数y=x+$\frac{1}{x}$(x>0)的最小值.
y=x+$\frac{1}{x}$=${(\sqrt{x})}^{2}$+${(\sqrt{\frac{1}{x}})}^{2}$=${(\sqrt{x})}^{2}$+${(\sqrt{\frac{1}{x}})}^{2}$-2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$+2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$=${(\sqrt{x}-\sqrt{\frac{1}{x})}}^{2}$+2
∵${({\sqrt{x}-\sqrt{\frac{1}{x}}})^2}$≥0,∴y≥2
∴当$\sqrt{x}$-$\sqrt{\frac{1}{x}}$=0,即x=1时,y最小值=2
请类比上面配方法,直接写出“问题情境”中的问题答案.
7.已知⊙A的半径长为2,⊙B的半径长为5,如果⊙A与⊙B内含,那么圆心距AB的长度可以为( )
| A. | 0 | B. | 3 | C. | 6 | D. | 9 |
4.口袋中装有形状、大小与质地都相同的红球2个,黄球1个,下列事件为随机事件的是( )
| A. | 随机摸出1个球,是白球 | B. | 随机摸出1个球,是红球 | ||
| C. | 随机摸出1个球,是红球或黄球 | D. | 随机摸出2个球,都是黄球 |
5.下列各式中计算正确的是( )
| A. | x2•x4=x6 | B. | x5+x52=3x10 | C. | (2a)3=6a3 | D. | m6÷m2=m3 |
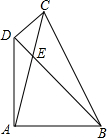 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=6,则AE=2$\sqrt{6}$.
如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=6,则AE=2$\sqrt{6}$.