题目内容
20.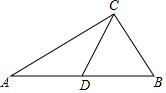 如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )
如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )| A. | $\frac{\sqrt{17}-1}{2}$ | B. | 2 | C. | 4$\sqrt{2}$-4 | D. | $\frac{4}{3}$$\sqrt{3}$ |
分析 根据已知条件得到AD=CD,根据相似三角形的性质得到$\frac{BC}{AB}=\frac{BD}{BC}$=$\frac{CD}{AC}$,设CD=x,BD=y,得到$\frac{2}{x+y}$=$\frac{y}{2}$=$\frac{x}{4}$,解方程组$\left\{\begin{array}{l}{xy+{y}^{2}=4}\\{4y=2x}\end{array}\right.$即可得到结论.
解答 解:∵△ACD是以AC为底的等腰三角形,
∴AD=CD,
∵△BCD与△BAC相似,
∴$\frac{BC}{AB}=\frac{BD}{BC}$=$\frac{CD}{AC}$,
设CD=x,BD=y,
∴$\frac{2}{x+y}$=$\frac{y}{2}$=$\frac{x}{4}$,
∴$\left\{\begin{array}{l}{xy+{y}^{2}=4}\\{4y=2x}\end{array}\right.$,
解得:x=2y,
∴y=$\frac{2\sqrt{3}}{3}$,
∴x=$\frac{4\sqrt{3}}{3}$,
∴CD=$\frac{4\sqrt{3}}{3}$,
故选D.
点评 本题考查了相似三角形的性质,根据相似三角形的性质得到方程组是解题的关键.

练习册系列答案
相关题目
9.在直角坐标系中,⊙A的半径为5厘米,圆心A的坐标为(-1,4),点P(3,-1)与⊙A的位置关系是( )
| A. | 在圆上 | B. | 在圆内 | C. | 在圆外 | D. | 无法确定 |
10. 问题情境
问题情境
已知矩形的面积为S(S为常数,S>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+$\frac{S}{x}$)(x>0)
探索研究
我们可以借鉴学习函数的经验,先探索函数y=x+$\frac{1}{x}$(x>0)的图象性质.
①列表:
表中m=$\frac{10}{3}$;
②描点:如图所示;
③连线:请在图中画出该函数的图象;
④观察图象,写出两条函数的性质;函数有最小值2;当x>1时,y随x的增大而增大
解决问题
在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.同样通过配方也可以求函数y=x+$\frac{1}{x}$(x>0)的最小值.
y=x+$\frac{1}{x}$=${(\sqrt{x})}^{2}$+${(\sqrt{\frac{1}{x}})}^{2}$=${(\sqrt{x})}^{2}$+${(\sqrt{\frac{1}{x}})}^{2}$-2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$+2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$=${(\sqrt{x}-\sqrt{\frac{1}{x})}}^{2}$+2
∵${({\sqrt{x}-\sqrt{\frac{1}{x}}})^2}$≥0,∴y≥2
∴当$\sqrt{x}$-$\sqrt{\frac{1}{x}}$=0,即x=1时,y最小值=2
请类比上面配方法,直接写出“问题情境”中的问题答案.
 问题情境
问题情境已知矩形的面积为S(S为常数,S>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+$\frac{S}{x}$)(x>0)
探索研究
我们可以借鉴学习函数的经验,先探索函数y=x+$\frac{1}{x}$(x>0)的图象性质.
①列表:
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{4}$ | m | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | $\frac{17}{4}$ | … |
②描点:如图所示;
③连线:请在图中画出该函数的图象;
④观察图象,写出两条函数的性质;函数有最小值2;当x>1时,y随x的增大而增大
解决问题
在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.同样通过配方也可以求函数y=x+$\frac{1}{x}$(x>0)的最小值.
y=x+$\frac{1}{x}$=${(\sqrt{x})}^{2}$+${(\sqrt{\frac{1}{x}})}^{2}$=${(\sqrt{x})}^{2}$+${(\sqrt{\frac{1}{x}})}^{2}$-2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$+2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$=${(\sqrt{x}-\sqrt{\frac{1}{x})}}^{2}$+2
∵${({\sqrt{x}-\sqrt{\frac{1}{x}}})^2}$≥0,∴y≥2
∴当$\sqrt{x}$-$\sqrt{\frac{1}{x}}$=0,即x=1时,y最小值=2
请类比上面配方法,直接写出“问题情境”中的问题答案.

 如图,在菱形ABCD中,∠B=120°,AB=4,点E是BC的中点,点F在CD边上,点C关于EF的对称点为C′,连接EC′,FC′,当点F从C运动到点D的过程中,AC′长度的最大值与最小值的差为4$\sqrt{3}$-2$\sqrt{7}$+2.
如图,在菱形ABCD中,∠B=120°,AB=4,点E是BC的中点,点F在CD边上,点C关于EF的对称点为C′,连接EC′,FC′,当点F从C运动到点D的过程中,AC′长度的最大值与最小值的差为4$\sqrt{3}$-2$\sqrt{7}$+2. 工人师傅盖房子时,常将房梁设计如图所示的图形,使其牢固不变形,这是利用三角形稳定性.
工人师傅盖房子时,常将房梁设计如图所示的图形,使其牢固不变形,这是利用三角形稳定性.
 如图,⊙O中,直径AB与弦CD相交,E是AC延长线上一点,连接BC、BD,且∠EBC=∠D.
如图,⊙O中,直径AB与弦CD相交,E是AC延长线上一点,连接BC、BD,且∠EBC=∠D.