题目内容
4.用如图所示的甲、乙、丙三块木板做一个长、宽、高分别为x厘米,y厘米和20厘米的长方体木箱,其中甲块木板锯成两块刚好能做箱底和一个长侧面,乙块木板刚好能做一个长侧面和一个短侧面,丙块木板刚好能做一个箱盖和剩下的一个短侧面(厚度忽略不计,x>y).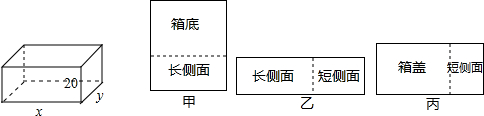
(1)用含x,y的代数式表示这三块木板的面积.
(2)若甲块木板的面积比丙块木板的面积大300平方厘米,乙块木板面积为1500平方厘米,求木箱的体积.
(3)如果购买一块长为100厘米,宽为(x+y)厘米的长方形木板做这个木箱,木板的利用率为$\frac{4}{5}$,试求$\frac{xy}{x+y}$的值.
分析 (1)利用展开图结合立体图形的边长进而得出答案;
(2)利用“甲块木板的面积比丙块木板的面积大300平方厘米,乙块木板面积为1500平方厘米”,结合(1)中所求得出等式求出即可;
(3)利用(1)中所求表示出箱子的侧面积,进而利用木板的利用率为$\frac{4}{5}$,得出等式求出即可.
解答 解:(1)由图可得:甲,xy+20x;乙:20x+20y;丙:xy+20y;
(2)由题意可得:$\left\{\begin{array}{l}{xy+20x-(xy+20y)=300}\\{20(x+y)=1500}\end{array}\right.$,
即$\left\{\begin{array}{l}{x-y=15}\\{x+y=75}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=45}\\{y=30}\end{array}\right.$,
故体积为:V=20xy=27000(cm3);
(3)由题意可得:$\frac{2xy+40(x+y)}{100(x+y)}$=$\frac{4}{5}$,
∴xy=20(x+y),
∴$\frac{xy}{x+y}$=20.
点评 此题主要考查了二元一次方程组的应用以及分式方程的应用,正确利用已知得出等量关系是解题关键.

练习册系列答案
相关题目
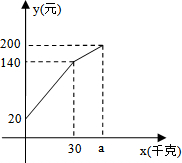 一农民带上若干千克自产的西红柿进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的西红柿千克数x与他手中持有的钱数y(含备用零钱)的关系,如图所示,结合图象回答下列问题.
一农民带上若干千克自产的西红柿进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的西红柿千克数x与他手中持有的钱数y(含备用零钱)的关系,如图所示,结合图象回答下列问题. 观察图形:它们是按一定规律排列的,依照此规律,第n个图形共有4n个圆点.
观察图形:它们是按一定规律排列的,依照此规律,第n个图形共有4n个圆点.