题目内容
14.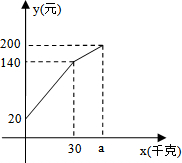 一农民带上若干千克自产的西红柿进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的西红柿千克数x与他手中持有的钱数y(含备用零钱)的关系,如图所示,结合图象回答下列问题.
一农民带上若干千克自产的西红柿进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的西红柿千克数x与他手中持有的钱数y(含备用零钱)的关系,如图所示,结合图象回答下列问题.(1)农民自带的零钱是多少?
(2)求降价前y与x之间的函数关系关系式.
(3)降价后他按每千克3元将剩余西红柿售完,这时他手中的钱(含备用零钱)是200元,试问他一共带了多少千克西红柿?
分析 (1)图象与y轴的交点就是农民自带的零钱.
(2)利用待定系数法求出0到30时线段的函数解析式即可.
(3)计算出降价后买的西红柿的数量,然后加上20千克即可求解.
解答 解:(1)农民自带的零钱是20元;
(2)设函数的解析式是y=kx+b,
则$\left\{\begin{array}{l}{b=20}\\{30k+b=140}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=4}\\{b=20}\end{array}\right.$.
则y与x的函数解析式是y=4x+20;
(3)(200-140)÷3=20(千克),
则他带的西红柿是30+20=50(千克).
50千克;
点评 主要考查利用一次函数的模型解决实际问题的能力和读图能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解,并会根据图示得出所需要的信息.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
4.当x=2时,代数式$\frac{3x-3}{{x}^{2}-1}$÷$\frac{3x}{x+1}$-$\frac{1}{x-1}$的结果是( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{3}{2}$ |
5.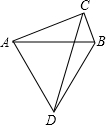 如图,以线段AB为边分别作直角三角形ABC和等边三角形ABD,其中∠ACB=90°.连接CD,当CD的长度最大时,此时∠CAB的大小是( )
如图,以线段AB为边分别作直角三角形ABC和等边三角形ABD,其中∠ACB=90°.连接CD,当CD的长度最大时,此时∠CAB的大小是( )
 如图,以线段AB为边分别作直角三角形ABC和等边三角形ABD,其中∠ACB=90°.连接CD,当CD的长度最大时,此时∠CAB的大小是( )
如图,以线段AB为边分别作直角三角形ABC和等边三角形ABD,其中∠ACB=90°.连接CD,当CD的长度最大时,此时∠CAB的大小是( )| A. | 75° | B. | 45° | C. | 30° | D. | 15° |
6.下列各式①$\sqrt{\frac{1}{2}}$;②$\sqrt{2x}$;③$\sqrt{{x}^{2}+{y}^{2}}$;④$\sqrt{-5}$;⑤$\root{3}{5}$,其中二次根式的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.某中学计划租用若干辆汽车运送七年级学生外出进行社会实践活动,如果一辆车乘坐35人,那么有25名学生没有车坐;如果一辆车乘坐45人,那么有一辆车只坐了25人,并且还空出一辆车.设计划租用x辆车,共有y名学生,则根据题意列方程组为( )
| A. | $\left\{\begin{array}{l}{35-25=y}\\{45(x-2)=y-25}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{35x=y-25}\\{45(x-2)+25=y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{35x+25=y}\\{45(x-1)+25=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{35x=y+25}\\{y-45(x-2)=25}\end{array}\right.$ |
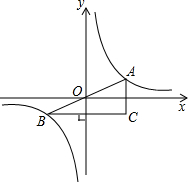 如图,A,B是函数y=$\frac{1}{x}$的图象上关于原点O对称的任意两点,AC平行于y轴,BC平行于x轴,则△ABC的面积为2.
如图,A,B是函数y=$\frac{1}{x}$的图象上关于原点O对称的任意两点,AC平行于y轴,BC平行于x轴,则△ABC的面积为2.