题目内容
9.抛物线y=(m+1)x2+(m2-1)x-2的顶点在y轴上,m=1.分析 根据二次函数的顶点在y轴上,顶点的横坐标为0列方程求解即可.
解答 解:∵抛物线y=(m+1)x2+(m2-1)x-2的顶点在y轴上,
∴-$\frac{b}{2a}$=-$\frac{{m}^{2}-1}{m+1}$=0,
∴m=±1且m≠-1,
∴m=1.
故答案为:1.
点评 本题考查了二次函数的性质,熟练掌握顶点坐标公式是解题的关键.

练习册系列答案
相关题目
1.计算(a3)3÷(-a2)4的结果是( )
| A. | a4 | B. | a3 | C. | a2 | D. | a |
18.已知点(1-2a,a-4)在第三象限,则整数a的值可以取的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19.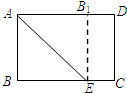 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )| A. | 1cm | B. | 2cm | C. | 4cm | D. | 6cm |
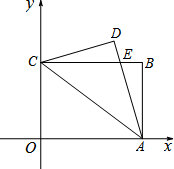 已知:如图,平面直角坐标系xOy中,矩形OABC的顶点A,C的坐标分别为(4,0),(0,3).将△OCA沿直线CA翻折,得到△DCA,且DA交CB于点E.
已知:如图,平面直角坐标系xOy中,矩形OABC的顶点A,C的坐标分别为(4,0),(0,3).将△OCA沿直线CA翻折,得到△DCA,且DA交CB于点E.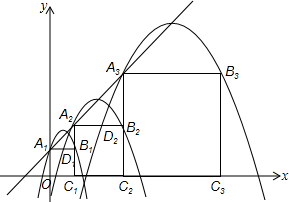 在平面直角坐标系中xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3…、An和点C1,C2,C3…、Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1、B1,且顶点在直线y=x+1上,抛物线L2过点A2、B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An、Bn,且顶点也在直线y=x+1上,其中抛物线L1交正方形A1B1C1O的边A1B1于点D1,抛物线L2交正方形A2B2C2C1的边A2B2于点D2…,抛物线Ln交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).
在平面直角坐标系中xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3…、An和点C1,C2,C3…、Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1、B1,且顶点在直线y=x+1上,抛物线L2过点A2、B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An、Bn,且顶点也在直线y=x+1上,其中抛物线L1交正方形A1B1C1O的边A1B1于点D1,抛物线L2交正方形A2B2C2C1的边A2B2于点D2…,抛物线Ln交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).