题目内容
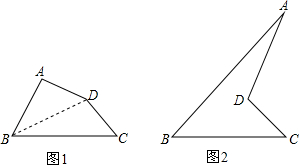
16.(1)如图①,在△ABC中,D、E分别是BC、AC边上的点,AD、BE交于点F,则∠1+∠2+∠3+∠C=180°.(2)如图②,D是△ABC的边AC上一点,E为BD上一点,则∠A,∠1,∠2之间的关系是∠2>∠1>∠A.

分析 (1)利用三角形的内角和和三角形的外角的性质解答即可;
(2)根据三角形的任何一个外角大于与它不相邻的一个内角解答.
解答 解:(1)∵∠ADC+∠3+∠C=180°,
∠ADC=∠1+∠2,
∴∠1+∠2+∠3+∠C=180°.
(2)在△CDE中,∠2>∠1,
在△ABD中,∠1>∠A,
∴∠2>∠1>∠A.
故答案为:180°,∠2>∠1>∠A.
点评 本题主要考查三角形的内角和定理,外角的性质,需要熟练掌握三角形的内角和为180°,任何一个外角大于与它不相邻的一个内角的性质.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
6.下列各式①$\sqrt{\frac{1}{2}}$;②$\sqrt{2x}$;③$\sqrt{{x}^{2}+{y}^{2}}$;④$\sqrt{-5}$;⑤$\root{3}{5}$,其中二次根式的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.计算(a3)3÷(-a2)4的结果是( )
| A. | a4 | B. | a3 | C. | a2 | D. | a |
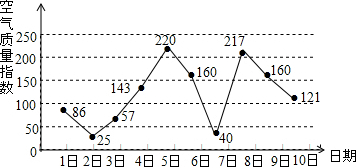 如图,气象局预报某市6月10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示重度污染.某人随机选择6月1日至6月8日中的某一天到达该市,并连续停留3天,则此人在该市停留期间遇到空气为重度污染的概率是$\frac{3}{4}$.
如图,气象局预报某市6月10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示重度污染.某人随机选择6月1日至6月8日中的某一天到达该市,并连续停留3天,则此人在该市停留期间遇到空气为重度污染的概率是$\frac{3}{4}$.