题目内容
4.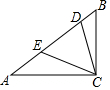 如图,在Rt△ABC的斜边AB上取两点D,E,使AD=AC,BE=BC.当∠B=60°时,求∠DCE的度数.
如图,在Rt△ABC的斜边AB上取两点D,E,使AD=AC,BE=BC.当∠B=60°时,求∠DCE的度数.
分析 根据三角形的内角和得到∠A=30°.根据等腰三角形的性质得到∠ACD=∠ADC=$\frac{1}{2}$(180°-∠A)=75°.推出△BCE是等边三角形,于是得到结论.
解答 解:∵∠ACB=90°,∠B=60°,
∴∠A=30°.
∵AD=AC,
∴∠ACD=∠ADC=$\frac{1}{2}$(180°-∠A)=75°.
∵BC=BE,∠B=60°,
∴△BCE是等边三角形,
∴∠BCE=60°,
∴∠DCE=∠ACD+∠BCE-∠ACB=75°+60°-90°=45°.
点评 本题考查了等腰三角形的性质,三角形的内角和,等边三角形的判定和性质,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.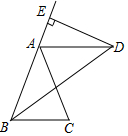 如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
(1)求证:AD∥BC;
(2)①若DE=6cm,求点D到BC的距离;
②当∠ABD=35°,∠DAC=2∠ABD时,求∠BAC的度数.
 如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.
如图,已知BD平分∠ABC,AB=AD,DE⊥AB,垂足为E.(1)求证:AD∥BC;
(2)①若DE=6cm,求点D到BC的距离;
②当∠ABD=35°,∠DAC=2∠ABD时,求∠BAC的度数.
9.下面计算正确的是( )
| A. | (-3)2=-9 | B. | (-2)3=-8 | C. | $\sqrt{16}$=±4 | D. | -$\root{3}{-8}$=-2 |
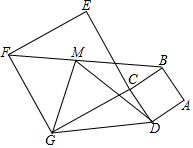 如图,正方形ABCD和正方形CEFG的面积分别为4平方厘米和36平方厘米,∠DCG=90°,M是BF的中点,则三角形DMG的面积为5平方厘米.
如图,正方形ABCD和正方形CEFG的面积分别为4平方厘米和36平方厘米,∠DCG=90°,M是BF的中点,则三角形DMG的面积为5平方厘米.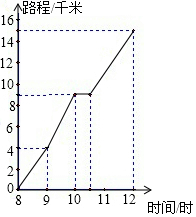 图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图象回答问题:
图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图象回答问题: