题目内容
15.一个多边形,除一个内角外,其余各内角之和等于2012°,求这个内角的度数及多边形的边数.分析 根据多边形内角和定理:(n-2)•180° (n≥3)且n为整数),可得:多边形的内角和一定是180°的倍数,而多边形的内角一定大于0°,并且小于180°,用2012除以180,根据商和余数的情况,求出这个多边形的边数与2的差是多少,即可求出这个多边形的边数,再用这个多边形的内角和减去2012°,求出这个内角的度数是多少即可.
解答 解:∵2012÷180=11…32,
∴这个多边形的边数与2的差是12,
∴这个多边形的边数是:12+2=14,
∴这个内角的度数是:
180°×12-2012°
=2160°-2012°
=148°
答:这个内角的度数为148°,多边形的边数为14.
点评 此题主要考查了多边形的内角和,要熟练掌握,解答此题的关键是要明确多边形内角和定理:(n-2)•180° (n≥3)且n为整数).

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
10.已知三角形的两边长分别为5和7,则第三边长不可能是( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
7.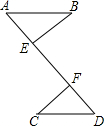 如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )
如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )
 如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )
如图,已知BE⊥AD,CF⊥AD,垂足分别为E、F,则在下列各组条件中选择一组,其中不能判定Rt△ABE≌Rt△DCF的是( )| A. | AB=DC,∠B=∠C | B. | AB=DC,AB∥CD | C. | AB=DC,BE=CF | D. | AB=DF,BE=CF |
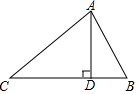 △ABC中,AC=15,AB=13,BC=14,则BC边上的高AD=12.
△ABC中,AC=15,AB=13,BC=14,则BC边上的高AD=12.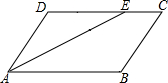 如图,在?ABCD中,∠BAD的平分线AE交边CD于点E,AB=5cm,BC=3cm,则EC=2cm.
如图,在?ABCD中,∠BAD的平分线AE交边CD于点E,AB=5cm,BC=3cm,则EC=2cm.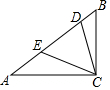 如图,在Rt△ABC的斜边AB上取两点D,E,使AD=AC,BE=BC.当∠B=60°时,求∠DCE的度数.
如图,在Rt△ABC的斜边AB上取两点D,E,使AD=AC,BE=BC.当∠B=60°时,求∠DCE的度数.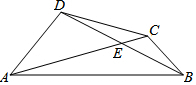 如图,四边形ABCD中,两对角线相交于E,且E为对角线BD的中点,∠DAE=30°,∠BCE=120°.若CE=1,BC=2,则AC的长为6.
如图,四边形ABCD中,两对角线相交于E,且E为对角线BD的中点,∠DAE=30°,∠BCE=120°.若CE=1,BC=2,则AC的长为6.