题目内容
20.下列一元二次方程中,没有实数根的是( )| A. | x2-2x-1=0 | B. | x2-2x+1=0 | C. | x2-1=0 | D. | x2+2x+3=0 |
分析 直接利用根的判别式的知识分别对各选项进行分析求解即可求得答案,注意排除法在解选择题中的应用.
解答 解:A、∵△=b2-4ac=(-2)2-4×1×(-1)=8>0,
∴有不相等的实数根;
B、∵△=b2-4ac=(-2)2-4×1×1=0,
∴有相等的实数根;
C、∵△=b2-4ac=02-4×1×(-1)=4>0,
∴有不相等的实数根;
D、∵△=b2-4ac=22-4×1×3=-8<0,
∴没有实数根.
故选D.
点评 此题考查了根的判别式.注意△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数根;△<0?方程没有实数根.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
8.已知二次函数y=-x2+6x-8.
(1)该函数图象的对称轴是x=3,顶点坐标(3,1);
(2)选取适当的数据填入下表,并描点画出函数图象;
(3)求抛物线与坐标轴的交点坐标;
(4)利用图象直接回答当x为何值时,函数值y大于0?
(1)该函数图象的对称轴是x=3,顶点坐标(3,1);
(2)选取适当的数据填入下表,并描点画出函数图象;
| x | … | … | |||||
| y | … | … |
(4)利用图象直接回答当x为何值时,函数值y大于0?
9.运用等式性质进行的变形,正确的是( )
| A. | 如果a=b,那么a+2=b+3 | B. | 如果a=b,那么ac=bc | ||
| C. | 如果a=b,那么$\frac{a}{c}=\frac{b}{c}$ | D. | 如果a2=3a,那么a=3 |
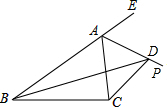 如图,D是△ABC的外角∠CAE平分线AP上一点,求证:DC+DB>AB+AC.
如图,D是△ABC的外角∠CAE平分线AP上一点,求证:DC+DB>AB+AC.