题目内容
19. A,B两地间的铁路线长828km,如图是一列慢车和一列快车沿相同路线从A地到B地所行驶的路程y(km)和行驶时间x(h)的变化的图象,根据图象回答下列问题:
A,B两地间的铁路线长828km,如图是一列慢车和一列快车沿相同路线从A地到B地所行驶的路程y(km)和行驶时间x(h)的变化的图象,根据图象回答下列问题:(1)慢车比快车早出发多少时间?快车比慢车早多少小时到达B地?
(2)分别求出表示快车、慢车行驶过程中路程y与时间x之间的函数关系式;
(3)快车出发多长时间才追上慢车?
(4)慢车出发多长时间后两车相距60km.(直接写出答案)
分析 (1)根据横纵坐标的意义,分别分析得出即可;
(2)分别利用待定系数法求出一次函数的解析式即可;
(3)利用两函数相等进而得出答案;
(4)需要分类讨论:快车没有出发;快车已经出发且快车没有到达目的地;快车已到目的地.
解答 解:(1)慢车比快车早出发2小时,快车比慢车早4小时到达;
(2)由图象可得:
设快车路程y1与时间x之间的函数表达式为:y1=kx+b,将(2,0),(14,828)代入得:
$\left\{\begin{array}{l}{2k+b=0}\\{14k+b=828}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=69}\\{b=-138}\end{array}\right.$,
故y1=69x-138;
设慢车路程y2与时间x之间的函数表达式为:y2=ax,将(18,828)代入得:
828=18a,
解得:a=46,
故y2=46x;
(3)当46x=69x-138,
解得:x=6,
故6-2=4(小时).
答:当快车出发4小时才追上慢车;
(4)当快车还没有出发时:$\frac{60}{46}=\frac{30}{23}$(h);
当快车出发后,快车还没有到达目的地时:69x-138-46x=60,解得:x=$\frac{198}{23}$;
当快车到达目的地后:14+$\frac{60}{23}$=15$\frac{7}{23}$.
综上所述,当慢车出发$\frac{30}{23}$h或$\frac{198}{23}$或15$\frac{7}{23}$时,两车相距60km.
点评 此题主要考查了一次函数的应用以及待定系数法求一次函数解析式,正确由图象得出正确信息是解题关键,另外,解答(3)题时,要分类讨论.

练习册系列答案
相关题目
8.已知二次函数y=-x2+6x-8.
(1)该函数图象的对称轴是x=3,顶点坐标(3,1);
(2)选取适当的数据填入下表,并描点画出函数图象;
(3)求抛物线与坐标轴的交点坐标;
(4)利用图象直接回答当x为何值时,函数值y大于0?
(1)该函数图象的对称轴是x=3,顶点坐标(3,1);
(2)选取适当的数据填入下表,并描点画出函数图象;
| x | … | … | |||||
| y | … | … |
(4)利用图象直接回答当x为何值时,函数值y大于0?
9.运用等式性质进行的变形,正确的是( )
| A. | 如果a=b,那么a+2=b+3 | B. | 如果a=b,那么ac=bc | ||
| C. | 如果a=b,那么$\frac{a}{c}=\frac{b}{c}$ | D. | 如果a2=3a,那么a=3 |
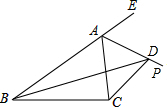 如图,D是△ABC的外角∠CAE平分线AP上一点,求证:DC+DB>AB+AC.
如图,D是△ABC的外角∠CAE平分线AP上一点,求证:DC+DB>AB+AC.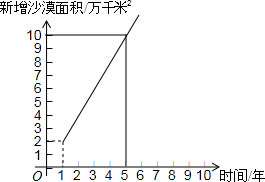 全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源己成为一项十分紧迫的任务,某地区现有土地面积100万千米2,沙漠面积200万千米2,土地沙漠化的变化情况如下图所示.
全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源己成为一项十分紧迫的任务,某地区现有土地面积100万千米2,沙漠面积200万千米2,土地沙漠化的变化情况如下图所示.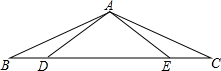 如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.
如图,点D,E在△ABC的边BC上,AB=AC,AD=AE. 如图,抛物线y=ax2+bx+4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
如图,抛物线y=ax2+bx+4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.