题目内容
11.计算:$\frac{1}{x(x+1)}$+$\frac{1}{(x+1)(x+2)}$+$\frac{1}{(x+2)(x+3)}$+…+$\frac{1}{(x+2015)(x+2016)}$,并求当x=1时,该代数式的值.分析 先利用$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$把各分式展开,然后合并即可得到原式=$\frac{2016}{x(x+2016)}$,然后把x=1代入计算即可.
解答 解:原式=$\frac{1}{x}$-$\frac{1}{x+1}$+$\frac{1}{x+1}$-$\frac{1}{x+2}$+$\frac{1}{x+2}$-$\frac{1}{x+3}$+…+$\frac{1}{x+2015}$-$\frac{1}{x+2016}$
=$\frac{1}{x}$-$\frac{1}{x+2016}$
=$\frac{x+2016-x}{x(x+2016)}$
=$\frac{2016}{x(x+2016)}$,
当x=1时,原式=$\frac{2016}{1×(1+2016)}$=$\frac{2016}{2017}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
1.下列选项中,不是同类项的是( )
| A. | 1与$\frac{1}{3}$ | B. | 2x2y与-2x2y | C. | -m2n与$\frac{7}{3}{n^2}m$ | D. | -2xm与与5xm |
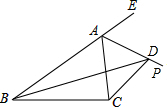 如图,D是△ABC的外角∠CAE平分线AP上一点,求证:DC+DB>AB+AC.
如图,D是△ABC的外角∠CAE平分线AP上一点,求证:DC+DB>AB+AC.