题目内容
世界上大部分国家都使用摄氏温度(℃),但美、英等国的天气预报仍然使用华氏温度(℉)两种计量之间有如下对应:
如果华氏温度y(℉)是摄氏温度x(℃)的一次函数.
(1)求出该一次函数表达式;
(2)求出华氏0度时摄氏约是多少度(精确到0.1℃);
(3)华氏温度的值可能小于其对应的摄氏温度的值吗?如果可能,请求出x的取值范围,如不可能,说明理由.
| 摄氏温度x | … | 0 | 10 | 20 | 30 | 40 | 50 | … |
| 华氏温度y | … | 32 | 50 | 68 | 86 | 104 | 122 | … |
(1)求出该一次函数表达式;
(2)求出华氏0度时摄氏约是多少度(精确到0.1℃);
(3)华氏温度的值可能小于其对应的摄氏温度的值吗?如果可能,请求出x的取值范围,如不可能,说明理由.
考点:一次函数的应用
专题:
分析:(1)设一次函数的解析式为y=kx+b,由待定系数法求出其解即可;
(2)当y=0时代入(1)的解析式求出其解即可;
(3)由华氏温度的值小于其对应的摄氏温度的值建立不等式求出其解即可.
(2)当y=0时代入(1)的解析式求出其解即可;
(3)由华氏温度的值小于其对应的摄氏温度的值建立不等式求出其解即可.
解答:解:(1)设一次函数的解析式为y=kx+b,由题意,得
,
解得:
,
∴y=1.8x+32.
答:一次函数表达式为y=1.8x+32;
(2)当y=0时,
1.8x+32=0,
解得:x=-
≈-18.9.
答:华氏0度时摄氏约是-18.9℃;
(3)由题意,得
1.8x+32<x,
解得:x<-
.
答:当x<-
时,华氏温度的值小于其对应的摄氏温度的值.
|
解得:
|
∴y=1.8x+32.
答:一次函数表达式为y=1.8x+32;
(2)当y=0时,
1.8x+32=0,
解得:x=-
| 160 |
| 9 |
答:华氏0度时摄氏约是-18.9℃;
(3)由题意,得
1.8x+32<x,
解得:x<-
| 320 |
| 17 |
答:当x<-
| 320 |
| 17 |
点评:本题考查了待定系数法求一次函数的解析式的运用,由函数值求自变量的值的运用,一元一次不等式的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
化简
×
的结果是( )
| 5 |
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,O是△ABC内一点,∠ACB=60°,∠α=∠β,则∠O=
如图,O是△ABC内一点,∠ACB=60°,∠α=∠β,则∠O= 如图,在△ABC中,E、F分别是AB、BC的中点,M、N是AC的三等分点,EM、FN的延长线相交于点D.求证:四边形ABCD是平行四边形.
如图,在△ABC中,E、F分别是AB、BC的中点,M、N是AC的三等分点,EM、FN的延长线相交于点D.求证:四边形ABCD是平行四边形.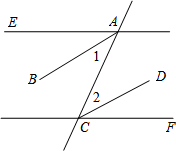 如图,直线AE、CF分别被直线AC所截,已知AE∥FC,AB平分∠EAC,CD平分∠ACF,将下列说明AB∥CD的过程及理由填写完整.
如图,直线AE、CF分别被直线AC所截,已知AE∥FC,AB平分∠EAC,CD平分∠ACF,将下列说明AB∥CD的过程及理由填写完整. 如图,已知AC∥FE,AD=FB,点A、D、B、F在一条直线上,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是
如图,已知AC∥FE,AD=FB,点A、D、B、F在一条直线上,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是 要建一个面积为48m2的矩形花圃,花圃的一边靠墙(墙上10m),并在平行于墙的一边开一个1m宽的门,现在可用的材料为19m长的篱笆,求花圃的长和宽.
要建一个面积为48m2的矩形花圃,花圃的一边靠墙(墙上10m),并在平行于墙的一边开一个1m宽的门,现在可用的材料为19m长的篱笆,求花圃的长和宽.